Python for Data Science Crash Course

Python for Data Science Crash Course#

Numpy#

Numpy is the reference library of scipy for scientific computing. The core of the library consists of numpy arrays which allow for easy handling of operations between vectors and matrices. Python arrays are generally tensors, which are numerical structures with a variable number of dimensions, and can therefore be one-dimensional arrays, two-dimensional matrices, or multi-dimensional structures (e.g., 10 x 10 x 10 cuboids). To use numpy arrays, we must first import the numpy package:

import numpy as np #the "as" notation allows us to reference the numpy namespace simply with np in the future

Numpy Arrays#

A multi-dimensional numpy array can be defined from a list of lists, as follows:

l = [[1,2,3],[4,5,2],[1,8,3]] #a list containing three lists
print("List of lists:",l) #it is displayed as we defined it
a = np.array(l) #I build a numpy array from the list of lists
print("Numpy array:\n",a) #each inner list is identified as a row of a two-dimensional matrix
print("Numpy array from tuple:\n",np.array(((1,2,3),(4,5,6)))) #I can also create numpy arrays from tuples

List of lists: [[1, 2, 3], [4, 5, 2], [1, 8, 3]]
Numpy array:
 [[1 2 3]
 [4 5 2]
 [1 8 3]]
Numpy array from tuple:
 [[1 2 3]
 [4 5 6]]

Question 1

What is an obvious advantage of NumPy arrays compared to lists, given the examples shown above?

Every numpy array has a shape property that allows us to determine the number of dimensions of the structure:

print(a.shape) #it is a 3 x 3 matrix

(3, 3)

Let’s look at some other examples:

array = np.array([1,2,3,4])
matrix = np.array([[1,2,3,4],[5,4,2,3],[7,5,3,2],[0,2,3,1]])
tensor = np.array([[[1,2,3,4],['a','b','c','d']],[[5,4,2,3],['a','b','c','d']],[[7,5,3,2],['a','b','c','d']],[[0,2,3,1],['a','b','c','d']]])
print('Array:',array, array.shape) # one-dimensional array, will have only one dimension
print('Matrix:\n',matrix, matrix.shape)
print('matrix:\n',tensor, tensor.shape) # tensor, will have two dimensions

Array: [1 2 3 4] (4,)
Matrix:
 [[1 2 3 4]
 [5 4 2 3]
 [7 5 3 2]
 [0 2 3 1]] (4, 4)
matrix:
 [[['1' '2' '3' '4']
  ['a' 'b' 'c' 'd']]

 [['5' '4' '2' '3']
  ['a' 'b' 'c' 'd']]

 [['7' '5' '3' '2']
  ['a' 'b' 'c' 'd']]

 [['0' '2' '3' '1']
  ['a' 'b' 'c' 'd']]] (4, 2, 4)

Question 2

In Numpy, is there a formal difference between a one-dimensional array and a matrix containing a single row (or a single column)?

Numpy arrays support element-by-element operations. Let’s look at the main operations of this type:

a1 = np.array([1,2,3,4]) 
a2 = np.array([4,3,8,1]) 
print("Sum:",a1+a2) #Vector sum
print("Elementwise multiplication:",a1*a2) #Element-wise multiplication
print("Power of two:",a1**2) #Square of elements
print("Elementwise power:",a1**a2) #Element-wise power
print("Scalar product:",a1.dot(a2)) #Vector scalar product
print("Minimum:",a1.min()) #Array minimum
print("Maximum:",a1.max()) #Array maximum
print("Sum:",a2.sum()) #Sum of all array values
print("Product:",a2.prod()) #Product of all array values
print("Mean:",a1.mean()) #Mean of all array values

Sum: [ 5  5 11  5]
Elementwise multiplication: [ 4  6 24  4]
Power of two: [ 1  4  9 16]
Elementwise power: [   1    8 6561    4]
Vector product: 38
Minimum: 1
Maximum: 4
Sum: 16
Product: 96
Mean: 2.5

Operations on matrices:

m1 = np.array([[1,2,3,4],[5,4,2,3],[7,5,3,2],[0,2,3,1]])
m2 = np.array([[8,2,1,4],[0,4,6,1],[4,4,2,0],[0,1,8,6]])

print("Sum:",m1+m2) #matrix sum
print("Elementwise product:\n",m1*m2) #element-wise product
print("Power of two:\n",m1**2) #square of elements
print("Elementwise power:\n",m1**m2) #element-wise power
print("Matrix multiplication:\n",m1.dot(m2)) #matrix multiplication
print("Minimum:",m1.min()) #minimum
print("Maximum:",m1.max()) #maximum
print("Minimum along columns:",m1.min(0)) #minimum along columns
print("Minimum along rows:",m1.min(1)) #minimum along rows
print("Sum:",m1.sum()) #sum of values
print("Mean:",m1.mean()) #mean value
print("Diagonal:",m1.diagonal()) #main diagonal of the matrix
print("Transposed:\n",m1.T) #transposed matrix

Sum: [[ 9  4  4  8]
 [ 5  8  8  4]
 [11  9  5  2]
 [ 0  3 11  7]]
Elementwise product:
 [[ 8  4  3 16]
 [ 0 16 12  3]
 [28 20  6  0]
 [ 0  2 24  6]]
Power of two:
 [[ 1  4  9 16]
 [25 16  4  9]
 [49 25  9  4]
 [ 0  4  9  1]]
Elementwise power:
 [[   1    4    3  256]
 [   1  256   64    3]
 [2401  625    9    1]
 [   1    2 6561    1]]
Matrix multiplication:
 [[20 26 51 30]
 [48 37 57 42]
 [68 48 59 45]
 [12 21 26  8]]
Minimum: 0
Maximum: 7
Minimum along columns: [0 2 2 1]
Minimum along rows: [1 2 2 0]
Sum: 47
Mean: 2.9375
Diagonal: [1 4 3 1]
Transposed:
 [[1 5 7 0]
 [2 4 5 2]
 [3 2 3 3]
 [4 3 2 1]]

Question 3

What is the advantage of using the operations illustrated above? What code would be needed to perform the operation a1**a2 if a1 and a2 were Python lists rather than numpy arrays?

Linspace, Arange, Zeros, Ones, Eye and Random#

The functions linspace, arange, zeros, ones, eye and random of numpy are useful for generating numeric arrays on the fly. In particular, the function linspace allows generating a sequence of n equally spaced numbers ranging from a minimum value to a maximum value:

a=np.linspace(10,20,5) # generates 5 equally spaced values ranging from 10 to 20
print(a)

[10.  12.5 15.  17.5 20. ]

arange is very similar to range, but directly returns a numpy array:

print(np.arange(10)) #numbers from 0 to 9
print(np.arange(1,6)) #numbers from 1 to 5
print(np.arange(0,7,2)) #even numbers from 0 to 6

[0 1 2 3 4 5 6 7 8 9]
[1 2 3 4 5]
[0 2 4 6]

Question 4

Is it possible to obtain the same result as arange using range? How?

We can create arrays containing zero or one of arbitrary shapes using zeros and ones:

print(np.zeros((3,4)))#zeros and ones take as a parameter a tuple containing the desired dimensions
print(np.ones((2,1)))

[[0. 0. 0. 0.]
 [0. 0. 0. 0.]
 [0. 0. 0. 0.]]
[[1.]
 [1.]]

The function eye allows you to create an identity square matrix:

print(np.eye(3))
print(np.eye(5))

[[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]
[[1. 0. 0. 0. 0.]
 [0. 1. 0. 0. 0.]
 [0. 0. 1. 0. 0.]
 [0. 0. 0. 1. 0.]
 [0. 0. 0. 0. 1.]]

To build an array of random values (uniform distribution) between 0 and 1 (zero included, one excluded), just write:

print(np.random.rand(5)) #an array with 5 random values between 0 and 1
print(np.random.rand(3,2)) #a 3x2 matrix of random values between 0 and 1

[0.4455531  0.15464262 0.73300802 0.83126699 0.4840601 ]
[[0.04519461 0.77306473]
 [0.81167333 0.33469426]
 [0.51806682 0.16306516]]

We can generate an array of random values normally (Gaussian) distributed with randn:

print(np.random.randn(5,2))

[[-0.27659656 -1.47446936]
 [ 0.30758864  0.95848991]
 [-0.18955928  0.98689232]
 [-1.06568839  0.79190779]
 [ 0.63691861 -1.36459616]]

We will talk in more detail about the Gaussian distribution later.

We can generate integers between a minimum (inclusive) and a maximum (exclusive) using randint:

print(np.random.randint(0,50,3))#three values between 0 and 50 (exclusive)
print(np.random.randint(0,50,(2,3)))#2x3 matrix of random integer values between 0 and 50 (exclusive)

[ 0 26 31]
[[ 7  9  8]
 [47  3 27]]

To generate random values reproducibly, you can specify a seed:

np.random.seed(123)
print(np.random.rand(5))

[0.69646919 0.28613933 0.22685145 0.55131477 0.71946897]

The code above (including the seed definition) returns the same results if rerun:

np.random.seed(123)
print(np.random.rand(5))

[0.69646919 0.28613933 0.22685145 0.55131477 0.71946897]

Question 5

What is the effect of re-running the previous cell changing the seed?

max, min, sum, argmax, argmin#

It is possible to calculate maxima and minima and sums of a matrix by rows and columns as follows:

mat = np.array([[1,-5,0],[4,3,6],[5,8,-7],[10,6,-12]])
print(mat)
print()
print( mat.max(0))# Column maximums
print()
print(mat.max(1))# Row maximums
print()
print (mat.min(0))# Column minimums
print()
print(mat.min(1))# Row minimums
print()
print(mat.sum(0))# Column sum
print()
print(mat.sum(1))# Row sum
print()
print(mat.max())# Global maximum
print(mat.min())# Global minimum
print(mat.sum())# Global sum

[[  1  -5   0]
 [  4   3   6]
 [  5   8  -7]
 [ 10   6 -12]]

[10  8  6]

[ 1  6  8 10]

[  1  -5 -12]

[ -5   3  -7 -12]

[ 20  12 -13]

[-4 13  6  4]

10
-12
19

It is also possible to obtain the indices at which there are maxima and minima using the argmax function:

print(mat.argmax(0))

[3 2 1]

We have a maximum in the fourth row in the first column, one in the third row in the second column, and one in the second row in the third column. Let’s verify it:

print(mat[3,0])
print(mat[2,1])
print(mat[1,2])
print(mat.max(0))

Similarly:

print(mat.argmax(1))
print(mat.argmin(0))
print(mat.argmin(1))

[0 2 1 0]
[0 0 3]
[1 1 2 2]

Indexing and Slicing#

Numpy arrays can be indexed in a similar way to Python lists:

arr = np.array([1,2,3,4,5])
print("arr[0]       ->",arr[0]) #first element of the array
print("arr[:3]      ->",arr[:3]) #first three elements
print("arr[1:5:2]   ->",arr[1:4:2]) #from the second to the fourth (inclusive) with a step of 2

arr[0]       -> 1
arr[:3]      -> [1 2 3]
arr[1:5:2]   -> [2 4]

When indexing an array with more than one dimension using a single index, the first dimension is automatically indexed. Let’s look at some examples with two-dimensional matrices:

mat = np.array(([1,5,2,7],[2,7,3,2],[1,5,2,1]))
print("Matrix:\n",mat,mat.shape) #matrix 3 x 4
print("mat[0]     ->",mat[0]) #a matrix is a collection of rows, so mat[0] returns the first row
print("mat[-1]     ->",mat[-1]) #last row
print("mat[::2]     ->",mat[::2]) #odd rows

Matrice:
 [[1 5 2 7]
 [2 7 3 2]
 [1 5 2 1]] (3, 4)
mat[0]     -> [1 5 2 7]
mat[-1]     -> [1 5 2 1]
mat[::2]     -> [[1 5 2 7]
 [1 5 2 1]]

Let’s see some examples with multi-dimensional tensors:

tens = np.array(([[1,5,2,7],
                [2,7,3,2],
                [1,5,2,1]],
                [[1,5,2,7],
                [2,7,3,2],
                [1,5,2,1]]))
print("Matrix:\n",tens,tens.shape) #tensor 2x3x4
print("tens[0]    ->",tens[0])#this is the first 3x4 matrix
print("tens[-1]    ->",tens[-1])#last 3x4 matrix

Matrice:
 [[[1 5 2 7]
  [2 7 3 2]
  [1 5 2 1]]

 [[1 5 2 7]
  [2 7 3 2]
  [1 5 2 1]]] (2, 3, 4)
tens[0]    -> [[1 5 2 7]
 [2 7 3 2]
 [1 5 2 1]]
tens[-1]    -> [[1 5 2 7]
 [2 7 3 2]
 [1 5 2 1]]

Indexing can continue through the other dimensions by specifying an additional index in square brackets or by separating the various indices with a comma:

mat = np.array(([1,5,2,7],[2,7,3,2],[1,5,2,1]))
print("Matrix:\n",mat,mat.shape) #matrix 3 x 4
print("mat[2][1]  ->",mat[2][1]) #third row, second column
print("mat[0,0]   ->",mat[0,0]) #first row, first column (more compact notation)

print("mat[0]     -> ",mat[0]) #returns the entire first row of the matrix
print("mat[:,0]   -> ",mat[:,0]) #returns the first column of the matrix.
                                #The two dots ":" mean "leave everything unchanged along this dimension"
print("mat[0,:]   ->",mat[0,:]) #alternative notation to get the first row of the matrix
print("mat[0:2,:] ->\n",mat[0:2,:]) #first two rows
print("mat[:,0:2] ->\n",mat[:,0:2]) #first two columns
print("mat[-1]    ->",mat[-1]) #last row

Matrice:
 [[1 5 2 7]
 [2 7 3 2]
 [1 5 2 1]] (3, 4)
mat[2][1]  -> 5
mat[0,0]   -> 1
mat[0]     ->  [1 5 2 7]
mat[:,0]   ->  [1 2 1]
mat[0,:]   -> [1 5 2 7]
mat[0:2,:] ->
 [[1 5 2 7]
 [2 7 3 2]]
mat[:,0:2] ->
 [[1 5]
 [2 7]
 [1 5]]
mat[-1]    -> [1 5 2 1]

Case of multi-dimensional tensors:

mat=np.array([[[1,2,3,4],['a','b','c','d']],
              [[5,4,2,3],['a','b','c','d']],
              [[7,5,3,2],['a','b','c','d']],
              [[0,2,3,1],['a','b','c','d']]]) 
print("mat[:,:,0] ->", mat[:,:,0]) #matrix contained in the "first channel" of the tensor
print("mat[:,:,1] ->",mat[:,:,1]) #matrix contained in the "second channel" of the tensor
print("mat[...,0] ->", mat[...,0]) #matrix contained in the "first channel" of the tensor (alternative notation)
print("mat[...,1] ->",mat[...,1]) #matrix contained in the "second channel" of the tensor (alternative notation)
#the "..." notation means "leave everything unchanged along the omitted dimensions"

mat[:,:,0] -> [['1' 'a']
 ['5' 'a']
 ['7' 'a']
 ['0' 'a']]
mat[:,:,1] -> [['2' 'b']
 ['4' 'b']
 ['5' 'b']
 ['2' 'b']]
mat[...,0] -> [['1' 'a']
 ['5' 'a']
 ['7' 'a']
 ['0' 'a']]
mat[...,1] -> [['2' 'b']
 ['4' 'b']
 ['5' 'b']
 ['2' 'b']]

Generally, when a subset of data is extracted from an array, it is referred to as slicing.

Question 6

Python lists do not support slicing. How can one implement a statement of the type a[2:8:2] using Python lists?

Logical Indexing and Slicing#

In numpy it is also possible to index arrays in a “logical” way, meaning by passing an array of boolean values as indices. For example, if we want to select the first and third value of an array, we must pass the array [True, False, True] as indices:

x = np.array([1,2,3])
print(x[np.array([True,False,True])]) # To select only 1 and 3
print(x[np.array([False,True,False])]) # To select only 2

[1 3]
[2]

Logical indexing is very useful when combined with the ability to build logical arrays “on the fly” by specifying a condition that array elements may or may not satisfy. For example:

x = np.arange(10)
print(x)
print(x>2) #generates an array of boolean values
#that will contain True for the values of x
#that satisfy the condition x>2
print(x==3) #True only for the value 3

[0 1 2 3 4 5 6 7 8 9]
[False False False  True  True  True  True  True  True  True]
[False False False  True False False False False False False]

By combining these two principles, it is simple to select only some values from an array, based on a condition:

x = np.arange(10)
print(x[x%2==0]) # selects even values
print(x[x%2!=0]) # selects odd values
print(x[x>2]) # selects values greater than 2

[0 2 4 6 8]
[1 3 5 7 9]
[3 4 5 6 7 8 9]

Question 7

Consider the two arrays a=np.array([1,2,3]) and b=np.array([5,2,4]). Use logical indexing to extract the numbers in a that are located at positions containing even values in b.

Reshape#

In some cases, it can be useful to change the “shape” of a matrix. For example, a 3x2 matrix can be modified by rearranging its elements to obtain a 2x3 matrix, a 1x6 matrix, or a 6x1 matrix. This can be done using the “reshape” method:

mat = np.array([[1,2],[3,4],[5,6]])
print(mat)
print(mat.reshape(2,3))
print(mat.reshape(1,6))
print(mat.reshape(6,1)) #matrix 6 x 1
print(mat.reshape(6)) #one-dimensional vector
print(mat.ravel())#equivalent to the previous one, but parameterless

[[1 2]
 [3 4]
 [5 6]]
[[1 2 3]
 [4 5 6]]
[[1 2 3 4 5 6]]
[[1]
 [2]
 [3]
 [4]
 [5]
 [6]]
[1 2 3 4 5 6]
[1 2 3 4 5 6]

We note that, if we read by rows (from left to right, from top to bottom), the order of the elements remains unchanged. We can also let numpy calculate one of the dimensions by replacing it with -1:

print(mat.reshape(2,-1))
print(mat.reshape(-1,6))

[[1 2 3]
 [4 5 6]]
[[1 2 3 4 5 6]]

Reshape can take as input the individual dimensions or a tuple containing the shape. In the latter case, it is convenient to perform operations of this kind:

mat1 = np.random.rand(3,2)
mat2 = np.random.rand(2,3)
print(mat2.reshape(mat1.shape)) # Give mat2 the same shape as mat1

[[0.72904971 0.43857224]
 [0.0596779  0.39804426]
 [0.73799541 0.18249173]]

Composing Arrays Using `concatenate` and `stack`#

Numpy allows combining different arrays using two main functions: concatenate and stack. The concatenate function takes as input a list (or tuple) of arrays and allows concatenating them along a specified existing dimension (axis), which by default is zero (row-wise concatenation):

a=np.arange(9).reshape(3,3)
print(a,a.shape,"\n")
cat=np.concatenate([a,a])
print(cat,cat.shape,"\n")
cat2=np.concatenate([a,a,a])
print(cat2,cat2.shape)

[[0 1 2]
 [3 4 5]
 [6 7 8]] (3, 3) 

[[0 1 2]
 [3 4 5]
 [6 7 8]
 [0 1 2]
 [3 4 5]
 [6 7 8]] (6, 3) 

[[0 1 2]
 [3 4 5]
 [6 7 8]
 [0 1 2]
 [3 4 5]
 [6 7 8]
 [0 1 2]
 [3 4 5]
 [6 7 8]] (9, 3)

It is possible to concatenate arrays along a different dimension by specifying it using the axis parameter:

a=np.arange(9).reshape(3,3)
print(a,a.shape,"\n")
cat=np.concatenate([a,a], axis=1) #column-wise concatenation
print(cat,cat.shape,"\n")
cat2=np.concatenate([a,a,a], axis=1) #column-wise concatenation
print(cat2,cat2.shape)

[[0 1 2]
 [3 4 5]
 [6 7 8]] (3, 3) 

[[0 1 2 0 1 2]
 [3 4 5 3 4 5]
 [6 7 8 6 7 8]] (3, 6) 

[[0 1 2 0 1 2 0 1 2]
 [3 4 5 3 4 5 3 4 5]
 [6 7 8 6 7 8 6 7 8]] (3, 9)

For the concatenation to be compatible, the arrays in the list must have the same dimensions along those that are not concatenated:

print(cat.shape,a.shape) #concatenation along axis 0, dimensions along other axes must be equal

(3, 6) (3, 3)

np.concatenate([cat,a], axis=0) #concatenation by columns #error!

The stack function, unlike concatenate, allows concatenating arrays along a new dimension. Compare the outputs of the two functions:

cat=np.concatenate([a,a])
print(cat,cat.shape)
stack=np.stack([a,a])
print(stack,stack.shape)

[[0 1 2]
 [3 4 5]
 [6 7 8]
 [0 1 2]
 [3 4 5]
 [6 7 8]] (6, 3)
[[[0 1 2]
  [3 4 5]
  [6 7 8]]

 [[0 1 2]
  [3 4 5]
  [6 7 8]]] (2, 3, 3)

In the case of stack, the arrays were concatenated along a new dimension. It is possible to specify alternative dimensions as in the case of concatenate:

stack=np.stack([a,a],axis=1)
print(stack,stack.shape)

[[[0 1 2]
  [0 1 2]]

 [[3 4 5]
  [3 4 5]]

 [[6 7 8]
  [6 7 8]]] (3, 2, 3)

In this case, the arrays have been concatenated along the second dimension.

stack=np.stack([a,a],axis=2)
print(stack,stack.shape)

[[[0 0]
  [1 1]
  [2 2]]

 [[3 3]
  [4 4]
  [5 5]]

 [[6 6]
  [7 7]
  [8 8]]] (3, 3, 2)

In this case, the arrays were concatenated along the last dimension.

Types#

Every numpy array has its type (see https://docs.scipy.org/doc/numpy-1.13.0/user/basics.types.html for the list of supported types). We can see the type of an array by inspecting the dtype property:

print(mat1.dtype)

float64

We can specify the type during array construction:

mat = np.array([[1,2,3],[4,5,6]],int)
print(mat.dtype)

int64

We can also change the type of an array on the fly using astype. This is useful, for example, if we want to perform a non-integer division:

print(mat/2)
print(mat.astype(float)/2)

[[0.5 1.  1.5]
 [2.  2.5 3. ]]
[[0.5 1.  1.5]
 [2.  2.5 3. ]]

Memory Management in Numpy#

Numpy manages memory dynamically for efficiency reasons. Therefore, an assignment or a slicing operation generally does not create a new copy of the data. Consider for example this code:

a=np.array([[1,2,3],[4,5,6]])
print(a)
b=a[0,0:2]
print(b)

[[1 2 3]
 [4 5 6]]
[1 2]

The slicing operation b=a[0,0:2] only allowed obtaining a new “view” of a part of a, but the data was not replicated in memory. Therefore, if we modify an element of b, the modification will actually be applied to a:

b[0]=-1
print(b)
print(a)

[-1  2]
[[-1  2  3]
 [ 4  5  6]]

To avoid this kind of behavior, it is possible to use the copy method which forces numpy to create a new copy of the data:

a=np.array([[1,2,3],[4,5,6]])
print(a)
b=a[0,0:2].copy()

print(b)
b[0]=-1
print(b)
print(a)

[[1 2 3]
 [4 5 6]]
[1 2]
[-1  2]
[[1 2 3]
 [4 5 6]]

In this new version of the code, a is no longer modified upon modification of b.

Broadcasting#

Numpy intelligently handles operations between arrays that have different shapes under certain conditions. Let’s look at a practical example: suppose we have a \(2\times3\) matrix and a \(1\times3\) array:

mat=np.array([[1,2,3],[4,5,6]],dtype=float)
arr=np.array([2,3,8])
print(mat)
print(arr)

[[1. 2. 3.]
 [4. 5. 6.]]
[2 3 8]

Now, suppose we want to divide, element by element, all the values of each row of the matrix by the values of the array. We can perform the required operation using a for loop:

mat2=mat.copy() # Copy the content of the matrix to not overwrite it
for i in range(mat2.shape[0]):# Indexes the rows
    mat2[i]=mat2[i]/arr
print(mat2)

[[0.5        0.66666667 0.375     ]
 [2.         1.66666667 0.75      ]]

arr.shape

(3,)

If we didn’t want to use for loops, we could replicate arr to obtain a \(2 \times 3\) matrix and then perform a simple element-wise division:

arr2=np.stack([arr,arr])
print(arr2)

print(mat/arr2)

[[2 3 8]
 [2 3 8]]
[[0.5        0.66666667 0.375     ]
 [2.         1.66666667 0.75      ]]

The same result can be obtained simply by asking numpy to divide mat by arr:

print(mat/arr)

[[0.5        0.66666667 0.375     ]
 [2.         1.66666667 0.75      ]]

This happens because numpy compares the dimensions of the two operands (\(2 \times 3\) and \(1 \times 3\)) and adapts the operand with the smaller shape to the one with the larger shape, by replicating its elements along the unit dimension (the first one). In practice, broadcasting generalizes operations between scalars and vectors/matrices like:

print(2*mat)
print(2*arr)

[[ 2.  4.  6.]
 [ 8. 10. 12.]]
[ 4  6 16]

In general, when operations are performed between two arrays, numpy compares the shapes dimension by dimension, from the last to the first. Two dimensions are compatible if:

They are equal;
One of them is equal to one.

Furthermore, the two shapes do not necessarily have to have the same number of dimensions.

For example, the following shapes are compatible:

\[\begin{split} 2 \times 3 \times 5 \\ 2 \times 3 \times 5 \end{split}\]

\[\begin{split} 2 \times 3 \times 5 \\ 2 \times 1 \times 5 \end{split}\]

\[\begin{split} 2 \times 3 \times 5 \\ 3 \times 5 \end{split}\]

\[\begin{split} 2 \times 3 \times 5 \\ 3 \times 1 \end{split}\]

Let’s see more examples of broadcasting:

mat1=np.array([[[1,3,5],[7,6,2]],[[6,5,2],[8,9,9]]])
mat2=np.array([[2,1,3],[7,6,2]])
print("Mat1 shape",mat1.shape)
print("Mat2 shape",mat2.shape)
print()
print("Mat1\n",mat1)
print()
print("Mat2\n",mat2)
print()
print("Mat1*Mat2\n",mat1*mat2)

Mat1 shape (2, 2, 3)
Mat2 shape (2, 3)

Mat1
 [[[1 3 5]
  [7 6 2]]

 [[6 5 2]
  [8 9 9]]]

Mat2
 [[2 1 3]
 [7 6 2]]

Mat1*Mat2
 [[[ 2  3 15]
  [49 36  4]]

 [[12  5  6]
  [56 54 18]]]

The product between the two tensors was performed by multiplying the two-dimensional matrices mat1[0,...] and mat2[0,...] by mat2. This is equivalent to repeating the elements of mat2 along the missing dimension and performing a point-by-point product between mat1 and the adapted version of mat2.

mat1=np.array([[[1,3,5],[7,6,2]],[[6,5,2],[8,9,9]]])
mat2=np.array([[[1,3,5]],[[6,5,2]]])
print("Mat1 shape",mat1.shape)
print("Mat2 shape",mat2.shape)
print()
print("Mat1\n",mat1)
print()
print("Mat2\n",mat2)
print()
print("Mat1*Mat2\n",mat1*mat2)

Mat1 shape (2, 2, 3)
Mat2 shape (2, 1, 3)

Mat1
 [[[1 3 5]
  [7 6 2]]

 [[6 5 2]
  [8 9 9]]]

Mat2
 [[[1 3 5]]

 [[6 5 2]]]

Mat1*Mat2
 [[[ 1  9 25]
  [ 7 18 10]]

 [[36 25  4]
  [48 45 18]]]

In this case, the product between the two tensors was obtained by multiplying all rows of the two-dimensional matrices mat1[0,...] by mat2[0] (first row of mat2) and all rows of the two-dimensional matrices mat1[1,...] by mat2[1] (second row of mat2). This is equivalent to repeating all elements of mat2 along the second dimension (the one containing \(1\)) and performing an element-wise product between mat1 and the adapted version of mat2.

Introduction to Matplotlib#

Matplotlib is the reference library for creating graphs in Python. It is a very powerful and well-documented library (https://matplotlib.org/). Let’s look at some classic examples of using the library.

2D plot#

Let’s see how to plot the function:

\[ y = x^2. \]

To plot the function, we will need to provide matplotlib with a series of \((x,y)\) value pairs that satisfy the equation shown above. The simplest way to do this is to:

Define an arbitrary vector of \(x\) values extracted from the function’s domain;
Calculate the respective \(y\) points using the analytical form shown above;
Plot the values using matplotlib.

The two vectors can be defined as follows:

import numpy as np

x = np.linspace(-100,100,300) # linearly sample 300 points between -100 and 100
y = x**2 # calculate the square of each point in x

Proceed to print:

from matplotlib import pyplot as plt #imports the pyplot module from matplotlib and calls it plt

plt.plot(x,y) #plots the x,y pairs as points in the Cartesian space
plt.xlabel('x') #sets a label for the x-axis
plt.ylabel('y') #sets a label for the y-axis
plt.title('My plot') #sets the title of the plot
plt.show() #shows the plot

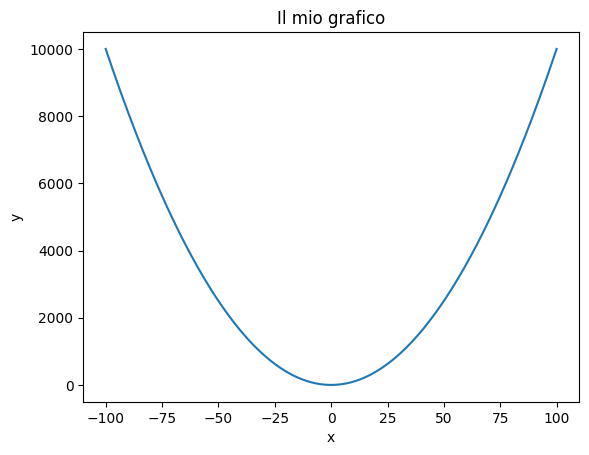
../_images/748a334c8fa426d74a4603d3b3fcd5a03c8747cad626f01780e6752b91d7d37d.png

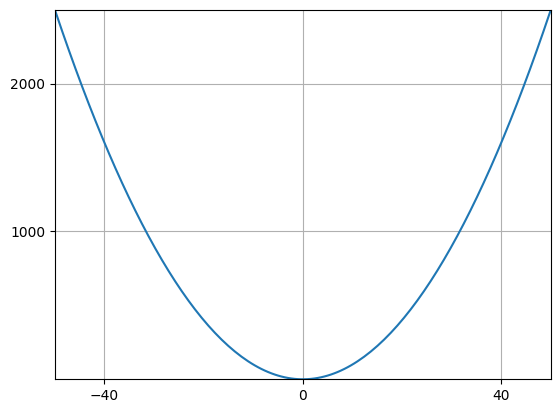
It is possible to control various aspects of the plot, including the limits of the x and y axes, the position of the “ticks” (the horizontal and vertical small lines on the axes) or adding a grid. Let’s see some examples:

plt.plot(x,y) #display the same plot
plt.xlim([-50,50]) #display x values only between -20 and 40
plt.ylim([0,2500]) #and y values only between 0 and 4000
plt.xticks([-40,0,40]) #insert only -40, 0 and 40 as "ticks" on the x-axis
plt.yticks([1000,2000]) #only 1000 and 2000 as y ticks
plt.grid() #add a grid
plt.show()

../_images/31b5184ed716612e8d7c3a9e1050b4997c4bef96fe155f1ff54ed2316be9700f.png

Subplot#

It can often be useful to compare different plots. To do this, we can make use of the subplot function, which allows us to construct a “grid of plots”.

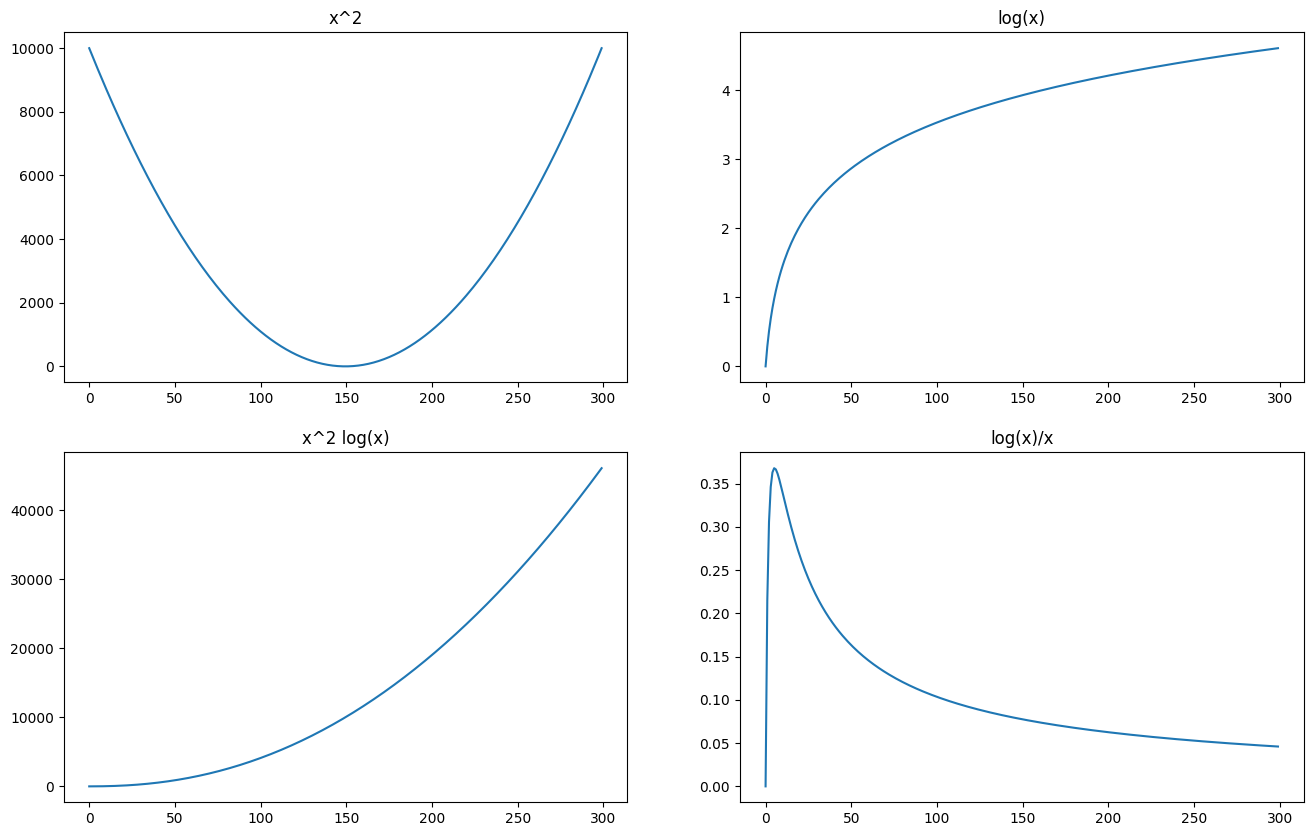
Let’s see, for example, how to plot the following functions in a 2 x 2 grid:

\[ y=x^2, \ \ \ y=log(x), \ \ \ y=x^2 \cdot log(x), \ \ \ y=log(x)/x \]

plt.figure(figsize=(16,10)) #defines a figure with a given size (in inches)
plt.subplot(2,2,1) #defines a 2x2 grid and selects the first cell as the current cell
x = np.linspace(-100,100,300)
plt.plot(x**2) #first graph
plt.title('x^2') #sets a title for the current cell

plt.subplot(2,2,2) #still in the same 2x2 grid, selects the second cell
x = np.linspace(1,100,300)
plt.plot(np.log(x)) #second graph
plt.title('log(x)') #sets a title for the current cell

plt.subplot(2,2,3) #selects the third cell
x = np.linspace(1,100,300)
plt.plot(x**2*np.log(x)) #third graph
plt.title('x^2 log(x)') #sets a title for the current cell

plt.subplot(2,2,4) #selects the fourth cell
x = np.linspace(1,100,300)
plt.plot(np.log(x)/x) #fourth graph
plt.title('log(x)/x') #sets a title for the current cell

plt.show() #shows the figure

../_images/805e66c91975c053cb568c94ca73b89882f3d0a16e7620616201eadb415a0bac.png

Colors and styles#

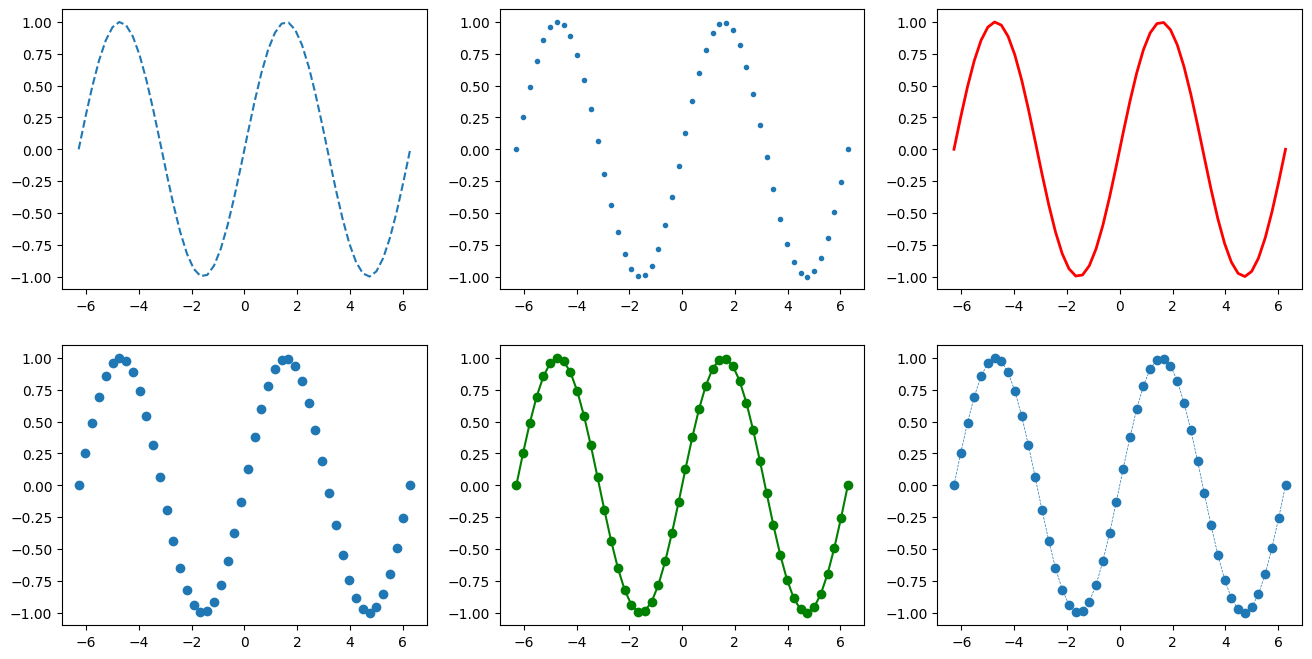
It is possible to use different colors and styles for the charts. Below are some examples:

x = np.linspace(-2*np.pi,2*np.pi,50)
y = np.sin(x)

plt.figure(figsize=(16,8))
plt.subplot(231) #abbreviated version of plt.subplot(2,3,1)
plt.plot(x,y,'--') #dashed line
plt.subplot(232)
plt.plot(x,y,'.') #only points
plt.subplot(233)
plt.plot(x,y,'r', linewidth=2) #red line, linewidth 2
plt.subplot(234)
plt.plot(x,y,'o') #circles
plt.subplot(235)
plt.plot(x,y,'o-g') #circles connected by green lines
plt.subplot(236)
plt.plot(x,y,'o--', linewidth=0.5) #circles connected by dashed lines, linewidth 0.5

plt.show()

../_images/e2c2425872911da283c3a6924206e01bacd6c555ba64e6f4c4cfa622b5eacb25.png

Line Overlay and Legend#

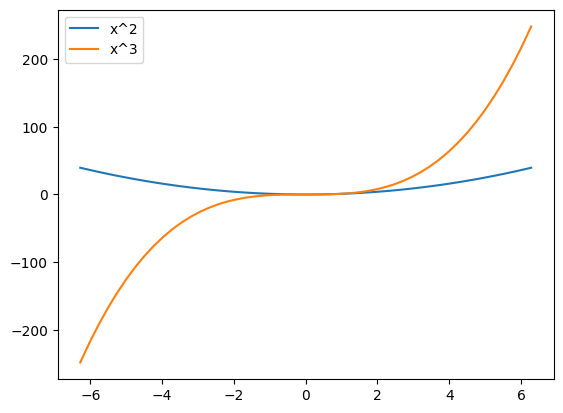
It’s simple to overlay multiple lines using matplotlib:

plt.figure()
plt.plot(x,x**2)
plt.plot(x,x**3) # For the second plot, matplotlib will automatically change color
plt.legend(['x^2','x^3']) # We can also add a legend.
# The legend elements will be associated with the lines in the order they were plotted
plt.show()

../_images/bac78a62404d3a6e8ecea5e5d763297ef34d6f130bde1990d7834d49a94ebbe5.png

Grids#

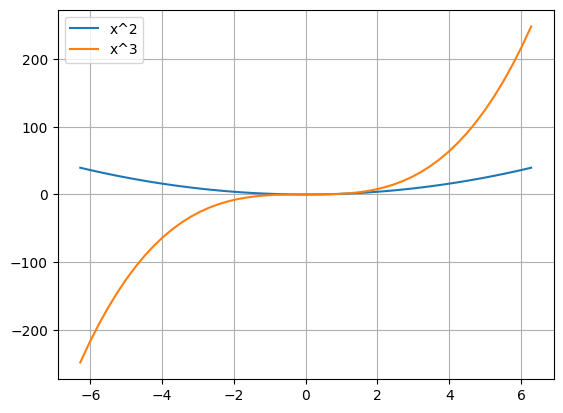
It is often useful to superimpose a grid on your plots. This can be done using plt.grid():

plt.figure()
plt.plot(x,x**2)
plt.plot(x,x**3) # For the second plot, matplotlib will automatically change color
plt.legend(['x^2','x^3']) # We can also add a legend.
# The legend elements will be associated with the lines in the order they were plotted
plt.grid()
plt.show()

../_images/b3beed067913fbf8f7e9352f7520a1ab521526697af4f5c9629b66838c8153f3.png

Matplotlib is a very versatile library. On Matplotlib’s official website, there is a gallery of plot examples with their respective code (https://matplotlib.org/stable/gallery/index.html). We will see in more detail how to obtain more complex visualizations during the course.

Introduction to Pandas#

We’ve seen how Python, combined with numpy and matplotlib, can be a powerful tool for scientific computing. However, there are other libraries that provide greater abstraction for easier data management and analysis. In this lab, we will cover the basics of the Pandas library, which is useful for data analysis. Specifically, we will see:

How to create and manage data series (Pandas Series);
How to create and manage Pandas DataFrames;
Examples of how to manipulate data in a DataFrame.

Pandas is a high-level library that provides various tools and data structures for data analysis. In particular, Pandas is very useful for loading, manipulating, and visualizing data quickly and conveniently before moving on to the actual analysis. The two main data structures in Pandas are Series and DataFrame.

Series#

A Series is a one-dimensional structure (a sequence of data) very similar to a NumPy array. Unlike it, its elements can be indexed using labels, as well as numbers. The values contained in a series can be of any type.

Creation of Series#

It is possible to define a Series starting from a list or a NumPy array:

import pandas as pd
import numpy as np
np.random.seed(123) # set a seed for reproducibility
s1 = pd.Series([7,5,2,8,9,6])# alternatively print(pd.Series(np.array([7,5,2])))
print(s1)

  7
  5
  2
  8
  9
  6
dtype: int64

The numbers displayed on the left represent the labels of the values contained in the series, which, by default, are numeric and sequential. When defining a series, you can specify appropriate labels (one for each value):

values = [7,5,2,8,9,6]
labels = ['a','b','c','d','e','f']
s2 = pd.Series(values, index=labels)
print(s2)

a    7
b    5
c    2
d    8
e    9
f    6
dtype: int64

It is possible to define a set also by means of a dictionary that specifies labels and values simultaneously:

s3=pd.Series({'a':14,'h':18,'m':72})
print(s3)

a    14
h    18
m    72
dtype: int64

Optionally, you can assign a name to a series:

pd.Series([1,2,3], name='My Series')

  1
  2
  3
Name: Mia Serie, dtype: int64

Question 1

What is the main difference between Pandas Series and Numpy array?

Indexing Series#

When the indices are numeric, Series can be indexed like numpy arrays:

print(s1[0]) #indexing
print(s1[0:4:2]) #slicing

7
0    7
2    2
dtype: int64

When indices are the most generic labels, indexing occurs similarly, but slicing cannot be used:

print(s2['c'])

Clearly, it is possible to modify the values in a series using indexing:

s2['c']=4
s2

a    7
b    5
c    4
d    8
e    9
f    6
dtype: int64

If the specified index does not exist, a new element will be created:

s2['z']=-2
s2

a    7
b    5
c    4
d    8
e    9
f    6
z   -2
dtype: int64

If we wanted to specify more than one label at a time, we could pass a list of labels:

print(s2[['a','c','d']])

a    7
c    4
d    8
dtype: int64

Series with alphanumeric labels can also be indexed by following the order in which data is entered into the series, in a sense “discarding” the alphanumeric labels and indexing the elements positionally. This effect is achieved using the iloc method:

print(s2,'\n')
print("Element at index 'a':",s2['a'])
print("First element of the series:",s2.iloc[0])

a    7
b    5
c    4
d    8
e    9
f    6
z   -2
dtype: int64 

Elemento di indice 'a': 7
Primo elemento della serie: 7

In certain cases, it can be useful to reset the index numbering. This can be done using the reset_index method:

print(s3,'\n')
print(s3.reset_index(drop=True)) # drop=True indicates to discard old indices

a    14
h    18
m    72
dtype: int64 

0    14
1    18
2    72
dtype: int64

Series also allow logical indexing:

print(s1,'\n') # series s1
print(s1>2,'\n') # logical indexing to select elements greater than 2
print(s1[s1>2],'\n') # application of logical indexing

  7
  5
  2
  8
  9
  6
dtype: int64 

   True
   True
  False
   True
   True
   True
dtype: bool 

  7
  5
  8
  9
  6
dtype: int64 

It is possible to specify the combination of two conditions using the logical operators “|” (or) and “&” (and), remembering to enclose the operands in parentheses:

(s1>2) & (s1<6)

  False
   True
  False
  False
  False
  False
dtype: bool

s1[(s1>2) & (s1<6)]

1    5
dtype: int64

Similarly for the or:

(s1<2) | (s1>6)

   True
  False
  False
   True
   True
  False
dtype: bool

print(s1[(s1<2) | (s1>6)])

  7
  8
  9
dtype: int64

As with NumPy arrays, memory allocation is dynamically managed for Series. Therefore, if I assign a series to a new variable and modify the second variable, the first one will also be modified:

s11=pd.Series([1,2,3])
s12=s11
s12[0]=-1
s11

 -1
  2
  3
dtype: int64

To obtain a new independent Series, we can use the copy method:

s11=pd.Series([1,2,3])
s12=s11.copy()
s12[0]=-1
s11

  1
  2
  3
dtype: int64

Question 2

What does the following code print to the screen?
s=pd.Series([1,2,3,4,6])
print(s[s%2])

Data Types#

Series can contain different data types:

pd.Series([2.5,3.4,5.2])

  2.5
  3.4
  5.2
dtype: float64

A Series is associated with a single data type. If we specify heterogeneous data types, the Series will be of type “object”:

s=pd.Series([2.5,'A',5.2])
s

  2.5
    A
  5.2
dtype: object

You can change the data type of a Series on the fly with astype in a similar way to how it’s done with Numpy arrays:

s=pd.Series([2,3,8,9,12,45])
print(s)
print(s.astype(float))

   2
   3
   8
   9
  12
  45
dtype: int64
   2.0
   3.0
   8.0
   9.0
  12.0
  45.0
dtype: float64

Question 3

Considering the Series defined as follows:
s=pd.Series([2.5,'A',5.2])
which of the following operations return an error? Why?
s.astype(str), s.astype(int)

Missing Data#

In Pandas, it’s possible to specify Series (and as we’ll see, DataFrames as well) with missing data. To indicate such values, the value np.nan is used:

missing = pd.Series([2,5,np.nan,8])
missing

  2.0
  5.0
  NaN
  8.0
dtype: float64

The NaN (not a number) values indicate values that can be missing for various reasons (e.g., data resulting from invalid operations, data that were not collected correctly, etc.).

In many cases, it can be useful to discard NaN data. This can be done with the dropna() operation:

missing.dropna()

  2.0
  5.0
  8.0
dtype: float64

Alternatively, we can replace NaN values with a specific value using fillna. We replace the NaNs with zero:

missing = pd.Series([2, 5, np.nan, 8])
print(missing)

missing.fillna(0)

  2.0
  5.0
  NaN
  8.0
dtype: float64

  2.0
  5.0
  0.0
  8.0
dtype: float64

Operations on and Between Series#

The main operations available for NumPy arrays are defined on Series:

print("Min:",s1.min())
print("Max:",s1.max())
print("Mean:",s1.mean())

Min: 2
Max: 9
Mean: 6.166666666666667

Let’s see how to replace missing values in a series with the average value:

data = pd.Series([1,5,2,np.nan,5,2,6,np.nan,9,2,3])
data

data.fillna(data.mean())

   1.000000
   5.000000
   2.000000
   3.888889
   5.000000
   2.000000
   6.000000
   3.888889
   9.000000
   2.000000
  3.000000
dtype: float64

Note that the mean function simply ignored the NaN values.

It is possible to obtain the size of a series using the len function:

print(len(s1))

It is possible to obtain statistics on the unique values (i.e. the values of the series, once duplicates have been removed) contained in a series using the unique method:

print("Unique:",s1.unique()) #returns unique values

Unique: [7 5 2 8 9 6]

To know the number of unique values in a series, we can use the nunique method:

s1.nunique()

It is possible to obtain the unique values of a series along with the frequencies with which they appear in the series using the value_counts method:

tmp = pd.Series(np.random.randint(0,10,100))
print(tmp.unique()) # unique values
tmp.value_counts() # unique values with their frequencies

[2 6 1 3 9 0 4 7 8 5]

  15
  14
  13
  10
  10
  10
  10
   8
   5
   5
Name: count, dtype: int64

The result of value_counts is a Series where the indices represent the unique values, and the values are the frequencies with which they appear in the series. The series is sorted by values.

The describe method allows you to calculate various statistics for the values contained in the series:

tmp.describe()

count    100.000000
mean       4.130000
std        2.830765
min        0.000000
25%        2.000000
50%        4.000000
75%        6.000000
max        9.000000
dtype: float64

In operations between series, elements are associated based on their indices. In the case where there is a perfect correspondence between elements, we obtain the following result:

print(pd.Series([1,2,3])+pd.Series([4,4,4]),'\n')
print(pd.Series([1,2,3])*pd.Series([4,4,4]),'\n')

  5
  6
  7
dtype: int64 

   4
   8
  12
dtype: int64 

In the event that some indices are missing, the corresponding boxes will be filled with NaN (not a number) to indicate the absence of the value:

s1 = pd.Series([1,4,2], index = [1,2,3])
s2 = pd.Series([4,2,8], index = [0,1,2])
print(s1,'\n')
print(s2,'\n')
print(s1+s2)

  1
  4
  2
dtype: int64 

  4
  2
  8
dtype: int64 

   NaN
   3.0
  12.0
   NaN
dtype: float64

In this case, index 0 was present only in the second series (s2), while index 3 was present only in the first series (s1).

If we want to exclude NaN values (including their indices) we can use the dropna method:

s3=s1+s2
print(s3)
print(s3.dropna())

   NaN
   3.0
  12.0
   NaN
dtype: float64
   3.0
  12.0
dtype: float64

It is possible to apply a function to all elements of a Series using the apply method. For example, let’s say we want to transform strings contained in a Series into uppercase. We can specify the str.upper function using the apply method:

s=pd.Series(['aba','cda','daf','acc'])
s.apply(str.upper)

  ABA
  CDA
  DAF
  ACC
dtype: object

Using apply we can also apply user-defined functions using lambda expressions or using the usual syntax:

def my_function(x):
    y="String: "
    return y+x
s.apply(my_function)

  Stringa: aba
  Stringa: cda
  Stringa: daf
  Stringa: acc
dtype: object

The same function can be written more compactly as a lambda expression:

s.apply(lambda x: "String: "+x)

  Stringa: aba
  Stringa: cda
  Stringa: daf
  Stringa: acc
dtype: object

It is possible to modify all occurrences of a given value in a Series using the replace method:

ser = pd.Series([1,2,15,-1,7,9,2,-1])
print(ser)
ser=ser.replace({-1:0}) # replace all occurrences of "-1" with zeros
print(ser)

   1
   2
  15
  -1
   7
   9
   2
  -1
dtype: int64
   1
   2
  15
   0
   7
   9
   2
   0
dtype: int64

Question 4

Try to apply the apply method to a Series, specifying a function that takes two arguments as input. Is it possible to do this? Why?

Conversion to Numpy Array#

It is possible to access the values of the series in the form of a numpy array using the values property:

print(s3.values)

[nan  3. 12. nan]

You need to be careful about the fact that values does not create an independent copy of the series, so if we modify the numpy array accessible via values, we are actually modifying the series as well:

a = s3.values
print(s3)
a[0]=-1
print(s3)

   NaN
   3.0
  12.0
   NaN
dtype: float64
  -1.0
   3.0
  12.0
   NaN
dtype: float64

Question 5

How can you obtain a Numpy array from a Series such that the two entities are independent?

DataFrame#

A DataFrame is essentially a table of numbers in which:

Each row represents a different observation;
Each column represents a variable.

Rows and columns can have names. In particular, it is very common to assign names to columns to indicate which variable each one corresponds to.

DataFrame Construction and Visualization#

It is possible to construct a DataFrame from a two-dimensional NumPy array (a matrix):

data = np.random.rand(10,3) # matrix of random values 10 x 3
# it's a matrix of 10 observations, each characterized by 3 variables

df = pd.DataFrame(data,columns=['A','B','C'])

df # in jupyter or in an ipython shell we can print the dataframe
# by simply writing "df". In a script we should write "print df"

	A	B	C
0	0.309884	0.507204	0.280793
1	0.763837	0.108542	0.511655
2	0.909769	0.218376	0.363104
3	0.854973	0.711392	0.392944
4	0.231301	0.380175	0.549162
5	0.556719	0.004135	0.638023
6	0.057648	0.043027	0.875051
7	0.292588	0.762768	0.367865
8	0.873502	0.029424	0.552044
9	0.240248	0.884805	0.460238

Each line has been automatically assigned a numerical index. If we wish, we can also specify names for the lines:

np.random.seed(123)#set a seed for repeatability
df = pd.DataFrame(np.random.rand(4,3),columns=['A','B','C'],index=['X','Y','Z','W'])
df

	A	B	C
X	0.696469	0.286139	0.226851
Y	0.551315	0.719469	0.423106
Z	0.980764	0.684830	0.480932
W	0.392118	0.343178	0.729050

Analogous to what was seen in the case of series, it is possible to construct a DataFrame using a dictionary that specifies the name and values of each column:

pd.DataFrame({'A':np.random.rand(10), 'B':np.random.rand(10), 'C':np.random.rand(10)})

	A	B	C
0	0.438572	0.724455	0.430863
1	0.059678	0.611024	0.493685
2	0.398044	0.722443	0.425830
3	0.737995	0.322959	0.312261
4	0.182492	0.361789	0.426351
5	0.175452	0.228263	0.893389
6	0.531551	0.293714	0.944160
7	0.531828	0.630976	0.501837
8	0.634401	0.092105	0.623953
9	0.849432	0.433701	0.115618

In the case of very large datasets, we can display only the first few rows using the head method:

df_big = pd.DataFrame(np.random.rand(100,3),columns=['A','B','C'])
df_big.head()

	A	B	C
0	0.317285	0.414826	0.866309
1	0.250455	0.483034	0.985560
2	0.519485	0.612895	0.120629
3	0.826341	0.603060	0.545068
4	0.342764	0.304121	0.417022

You can also specify the number of lines to display:

df_big.head(2)

	A	B	C
0	0.317285	0.414826	0.866309
1	0.250455	0.483034	0.985560

In a similar way, we can show the last lines with tail:

df_big.tail(3)

	A	B	C
97	0.811953	0.335544	0.349566
98	0.389874	0.754797	0.369291
99	0.242220	0.937668	0.908011

We can obtain the number of rows of the DataFrame using the len function:

print(len(df_big))

If we want to know both the number of rows and the number of columns, we can call the shape property:

print(df_big.shape)

(100, 3)

Analogous to what was seen for Series, we can view a DataFrame as a numpy array by calling the values property:

print(df,'\n')
print(df.values)

          A         B         C
X  0.696469  0.286139  0.226851
Y  0.551315  0.719469  0.423106
Z  0.980764  0.684830  0.480932
W  0.392118  0.343178  0.729050 

[[0.69646919 0.28613933 0.22685145]
 [0.55131477 0.71946897 0.42310646]
 [0.9807642  0.68482974 0.4809319 ]
 [0.39211752 0.34317802 0.72904971]]

The same considerations about memory made for Series also apply to DataFrames. To obtain an independent copy of a DataFrame, you can use the copy method:

df2=df.copy()

Question 6

In what way does a DataFrame mainly differ from a two-dimensional Numpy array? What is the advantage of DataFrames?

Indexing#

Pandas provides a range of tools for indexing DataFrames by selecting rows or columns. For example, we can select column B as follows:

s = df['B']
print(s, '\n')
print("Type of s:", type(s))

X    0.286139
Y    0.719469
Z    0.684830
W    0.343178
Name: B, dtype: float64 

Tipo di s: <class 'pandas.core.series.Series'>

It should be noted that the result of this operation is a Series (a DataFrame is fundamentally a collection of Series, each representing a column) which has the name of the considered column as its name. We can select more than one row by specifying a list of rows:

dfAB = df[['A','C']]
dfAB

	A	C
X	0.696469	0.226851
Y	0.551315	0.423106
Z	0.980764	0.480932
W	0.392118	0.729050

The result of this operation is instead a DataFrame. Row selection is done using the loc property:

df5 = df.loc['X']
df5

A    0.696469
B    0.286139
C    0.226851
Name: X, dtype: float64

The result of this operation is also a Series, but in this case the indices represent the column names, while the name of the series corresponds to the index of the selected row. As with Series, we can use iloc to index rows positionally:

df.iloc[1] #equivalent to df.loc['Y']

A    0.551315
B    0.719469
C    0.423106
Name: Y, dtype: float64

It is also possible to chain indexing operations to select a specific value:

print(df.iloc[1]['A'])
print(df['A'].iloc[1])

0.5513147690828912
0.5513147690828912

Even in this case, we can use logical indexing in a similar way to what we saw for numpy:

df_big2=df_big[df_big['C']>0.5]
print(len(df_big), len(df_big2))
df_big2.head() # some indices are missing as the corresponding rows have been removed

100 53

	A	B	C
0	0.317285	0.414826	0.866309
1	0.250455	0.483034	0.985560
3	0.826341	0.603060	0.545068
5	0.681301	0.875457	0.510422
6	0.669314	0.585937	0.624904

It’s possible to combine what we’ve seen so far to manipulate data simply and quickly. Let’s assume we want to select rows for which the sum of the values in B and C is less than \(0.7\), and let’s assume we are only interested in the A values of those rows (and not the entire row of A, B, C values). The result we expect is a one-dimensional array of values. We can obtain the desired result as follows:

average_result = df[(df['B'] + df['C']) > 0.7]['A']
print(average_result.head(), average_result.shape)

Y    0.551315
Z    0.980764
W    0.392118
Name: A, dtype: float64 (3,)

We can apply indexing also at the level of the entire table (in addition to the level of individual columns):

df>0.3

	A	B	C
X	True	False	False
Y	True	True	True
Z	True	True	True
W	True	True	True

If we apply this indexing to the DataFrame, we will get the appearance of some NaNs, which indicate the presence of elements that do not respect the condition considered:

df[df>0.3]

	A	B	C
X	0.696469	NaN	NaN
Y	0.551315	0.719469	0.423106
Z	0.980764	0.684830	0.480932
W	0.392118	0.343178	0.729050

We can remove NaN values using the dropna method, as seen in the case of Series. However, in this case, all rows that have at least one NaN will be removed:

df[df>0.3].dropna()

	A	B	C
Y	0.551315	0.719469	0.423106
Z	0.980764	0.684830	0.480932
W	0.392118	0.343178	0.729050

We can ask dropna to remove columns with at least one NaN by specifying axis=1:

df[df>0.3].dropna(axis=1)

	A
X	0.696469
Y	0.551315
Z	0.980764
W	0.392118

Alternatively, we can replace the NaN values on the fly using the fillna function:

df[df>0.3].fillna('VAL') #replaces NaNs with 'VAL'

	A	B	C
X	0.696469	VAL	VAL
Y	0.551315	0.719469	0.423106
Z	0.980764	0.68483	0.480932
W	0.392118	0.343178	0.72905

Even in this case, as seen with Series, we can restore the order of the indices using the reset_index method:

print(df)
print(df.reset_index(drop=True))

          A         B         C
X  0.696469  0.286139  0.226851
Y  0.551315  0.719469  0.423106
Z  0.980764  0.684830  0.480932
W  0.392118  0.343178  0.729050
          A         B         C
0  0.696469  0.286139  0.226851
1  0.551315  0.719469  0.423106
2  0.980764  0.684830  0.480932
3  0.392118  0.343178  0.729050

If we don’t specify drop=True, the old indices will be maintained as a new column:

print(df.reset_index())

  index         A         B         C
   X  0.696469  0.286139  0.226851
   Y  0.551315  0.719469  0.423106
   Z  0.980764  0.684830  0.480932
   W  0.392118  0.343178  0.729050

We can set any column as the new index. For example:

df.set_index('A')

	B	C
A
0.696469	0.286139	0.226851
0.551315	0.719469	0.423106
0.980764	0.684830	0.480932
0.392118	0.343178	0.729050

It should be noted that this operation does not actually modify the DataFrame, but creates a new “view” of the data with the requested modification:

```python
import pandas as pd

# Crea un DataFrame di esempio
dati = {
    'nome_prodotto': ['Mela', 'Banana', 'Arancia', 'Mela', 'Banana'],
    'prezzo_unitario': [1.2, 0.5, 0.8, 1.3, 0.6],
    'quantita_venduta': [100, 150, 120, 80, 200]
}
df = pd.DataFrame(dati)

# Calcola il prezzo totale per ogni prodotto
df['prezzo_totale'] = df['prezzo_unitario'] * df['quantita_venduta']

# Calcola la media delle quantità vendute
media_quantita = df['quantita_venduta'].mean()
print(f"Quantità venduta media: {media_quantita}")

# Trova il prodotto più costoso
prodotto_piu_costoso = df.loc[df['prezzo_unitario'].idxmax()]
print("\nProdotto più costoso:")
print(prodotto_piu_costoso)

# Filtra i prodotti con quantità venduta maggiore di 100
prodotti_ad_alta_vendita = df[df['quantita_venduta'] > 100]
print("\nProdotti con vendita elevata:")
print(prodotti_ad_alta_vendita)

# Raggruppa per nome prodotto e calcola la somma delle quantità vendute
vendite_per_prodotto = df.groupby('nome_prodotto')['quantita_venduta'].sum()
print("\nVendite totali per prodotto:")
print(vendite_per_prodotto)
```

	A	B	C
X	0.696469	0.286139	0.226851
Y	0.551315	0.719469	0.423106
Z	0.980764	0.684830	0.480932
W	0.392118	0.343178	0.729050

To use this modified version of the dataframe, we can save it in another variable:

df2=df.set_index('A')
df2

	B	C
A
0.696469	0.286139	0.226851
0.551315	0.719469	0.423106
0.980764	0.684830	0.480932
0.392118	0.343178	0.729050

Question 7

Consider the following DataFrame:
pd.DataFrame({'A':[1,2,3,4],'B':[3,2,6,7],'C':[0,2,-1,12]})
Use logical indexing to select the rows where the sum of the values in ‘C’ and ‘A’ is greater than \(1\).

DataFrame Manipulation#

The values contained in the rows and columns of the dataframe can be easily modified. The following example multiplies all values in column B by 2:

df['B'] *= 2
df.head()

	A	B	C
X	0.696469	0.572279	0.226851
Y	0.551315	1.438938	0.423106
Z	0.980764	1.369659	0.480932
W	0.392118	0.686356	0.729050

Similarly, we can divide all the values in row with index 2 by 3:

df.iloc[2]=df.iloc[2]/3
df.head()

	A	B	C
X	0.696469	0.572279	0.226851
Y	0.551315	1.438938	0.423106
Z	0.326921	0.456553	0.160311
W	0.392118	0.686356	0.729050

We can define a new column with a simple assignment operation:

df['D'] = df['A'] + df['C']
df['E'] = np.ones(len(df))*5
df.head()

	A	B	C	D	E
X	0.696469	0.572279	0.226851	0.923321	5.0
Y	0.551315	1.438938	0.423106	0.974421	5.0
Z	0.326921	0.456553	0.160311	0.487232	5.0
W	0.392118	0.686356	0.729050	1.121167	5.0

We can remove a column using the drop method and specifying axis=1 to indicate that we want to remove a column:

df.drop('E',axis=1).head()

	A	B	C	D
X	0.696469	0.572279	0.226851	0.923321
Y	0.551315	1.438938	0.423106	0.974421
Z	0.326921	0.456553	0.160311	0.487232
W	0.392118	0.686356	0.729050	1.121167

The drop method does not modify the DataFrame but only generates a new “view” without the column to be removed:

df.head()

	A	B	C	D	E
X	0.696469	0.572279	0.226851	0.923321	5.0
Y	0.551315	1.438938	0.423106	0.974421	5.0
Z	0.326921	0.456553	0.160311	0.487232	5.0
W	0.392118	0.686356	0.729050	1.121167	5.0

We can actually remove the column by an assignment:

df=df.drop('E',axis=1)
df.head()

	A	B	C	D
X	0.696469	0.572279	0.226851	0.923321
Y	0.551315	1.438938	0.423106	0.974421
Z	0.326921	0.456553	0.160311	0.487232
W	0.392118	0.686356	0.729050	1.121167

The removal of rows happens in the same way, but you need to specify axis = 0:

df.drop('X', axis=0)

	A	B	C	D
Y	0.551315	1.438938	0.423106	0.974421
Z	0.326921	0.456553	0.160311	0.487232
W	0.392118	0.686356	0.729050	1.121167

It is also possible to add a new row at the end of the DataFrame using the append method. Since the rows of a DataFrame are Series, we will need to construct a series with the correct indices (corresponding to the DataFrame’s columns) and the correct name (corresponding to the new index):

new_row=pd.Series([1,2,3,4], index=['A','B','C','D'], name='H')
print(new_row)
df.append(new_row)

A    1
B    2
C    3
D    4
Name: H, dtype: int64

	A	B	C	D
X	0.696469	0.572279	0.226851	0.923321
Y	0.551315	1.438938	0.423106	0.974421
Z	0.326921	0.456553	0.160311	0.487232
W	0.392118	0.686356	0.729050	1.121167
H	1.000000	2.000000	3.000000	4.000000

We can add more than one row at a time by specifying a DataFrame:

new_rows = pd.DataFrame({'A':[0,1],'B':[2,3],'C':[4,5],'D':[6,7]}, index=['H','K'])
new_rows

	A	B	C	D
H	0	2	4	6
K	1	3	5	7

df.append(new_rows)

	A	B	C	D
X	0.696469	0.572279	0.226851	0.923321
Y	0.551315	1.438938	0.423106	0.974421
Z	0.326921	0.456553	0.160311	0.487232
W	0.392118	0.686356	0.729050	1.121167
H	0.000000	2.000000	4.000000	6.000000
K	1.000000	3.000000	5.000000	7.000000

Question 8

Consider the following DataFrame:
pd.DataFrame({'A':[1,2,3,4],'B':[3,2,6,7],'C':[0,2,-1,12]})
Insert a new column ‘D’ into the DataFrame that contains the value \(1\) in all rows where the value of B is greater than the value of C.

Hint: use “astype(int)” to transform booleans into integers.

Operations between and on DataFrames#

The operations seen in the case of Series remain defined on DataFrames, with the appropriate differences. Generally, these are applied to all columns of the DataFrame independently:

df.mean() # mean of each column

A    0.491706
B    0.788531
C    0.384830
D    0.876535
dtype: float64

df.max() # maximum of each column

A    0.696469
B    1.438938
C    0.729050
D    1.121167
dtype: float64

df.describe() #statistics for each column

	A	B	C	D
count	4.000000	4.000000	4.000000	4.000000
mean	0.491706	0.788531	0.384830	0.876535
std	0.165884	0.443638	0.255159	0.272747
min	0.326921	0.456553	0.160311	0.487232
25%	0.375818	0.543347	0.210216	0.814298
50%	0.471716	0.629317	0.324979	0.948871
75%	0.587603	0.874502	0.499592	1.011108
max	0.696469	1.438938	0.729050	1.121167

Since the columns of a DataFrame are Series, the apply method can be applied to them:

df['A']=df['A'].apply(lambda x: "Number: "+str(x))
df

	A	B	C	D
X	Numero: 0.6964691855978616	0.572279	0.226851	0.923321
Y	Numero: 0.5513147690828912	1.438938	0.423106	0.974421
Z	Numero: 0.3269213994615385	0.456553	0.160311	0.487232
W	Numero: 0.3921175181941505	0.686356	0.729050	1.121167

It is possible to sort the rows of a DataFrame by the values of one of the columns using the sort_values method:

df.sort_values(by='D')

	A	B	C	D
Z	Numero: 0.3269213994615385	0.456553	0.160311	0.487232
X	Numero: 0.6964691855978616	0.572279	0.226851	0.923321
Y	Numero: 0.5513147690828912	1.438938	0.423106	0.974421
W	Numero: 0.3921175181941505	0.686356	0.729050	1.121167

To make the sorting permanent, we need to perform an assignment:

df=df.sort_values(by='D')
df

	A	B	C	D
Z	Numero: 0.3269213994615385	0.456553	0.160311	0.487232
X	Numero: 0.6964691855978616	0.572279	0.226851	0.923321
Y	Numero: 0.5513147690828912	1.438938	0.423106	0.974421
W	Numero: 0.3921175181941505	0.686356	0.729050	1.121167

Question 9

Consider the following DataFrame:
pd.DataFrame({'A':[1,2,3,4],'B':[3,2,6,7],'C':[0,2,-1,12]})
Transform the “B” column so that the new values are:

equal to zero if previously even;

equal to -1 if previously odd.

Remove Rows and Columns#

You can remove a row or a column from a DataFrame:

data = pd.DataFrame({'A':[1,2,3,4],'B':[3,2,6,7],'C':[0,2,-1,12]})
print(data)

data.drop(1) # remove row 1
data.drop('B', axis=1) # remove column B

	A	C
0	1	0
1	2	2
2	3	-1
3	4	12

Please note that the operations shown above do not modify the original array, but return a modified copy of it:

data = pd.DataFrame({'A':[1,2,3,4],'B':[3,2,6,7],'C':[0,2,-1,12]})
print(data)

data.drop(1) # remove row 1
data

	A	B	C
0	1	3	0
1	2	2	2
2	3	6	-1
3	4	7	12

We can perform a persistent modification using inplace=True:

data = pd.DataFrame({'A':[1,2,3,4],'B':[3,2,6,7],'C':[0,2,-1,12]})
print(data)

data.drop(1, inplace=True) # remove row 1
data

	A	B	C
0	1	3	0
2	3	6	-1
3	4	7	12

Or more explicitly as follows:

data = pd.DataFrame({'A':[1,2,3,4],'B':[3,2,6,7],'C':[0,2,-1,12]})
print(data)

data = data.drop(1) # remove row 1
data

	A	B	C
0	1	3	0
2	3	6	-1
3	4	7	12

Groupby#

The groupby method allows you to group the rows of a DataFrame and call aggregate functions on them. Let’s consider a more representative DataFrame:

df=pd.DataFrame({'income':[10000,11000,9000,3000,1000,5000,7000,2000,7000,12000,8000],\
                 'age':[32,32,45,35,28,18,27,45,39,33,32],\
                 'sex':['M','F','M','M','M','F','F','M','M','F','F'],\
                 'company':['CDX','FLZ','PTX','CDX','PTX','CDX','FLZ','CDX','FLZ','PTX','FLZ']})
df

	income	age	sex	company
0	10000	32	M	CDX
1	11000	32	F	FLZ
2	9000	45	M	PTX
3	3000	35	M	CDX
4	1000	28	M	PTX
5	5000	18	F	CDX
6	7000	27	F	FLZ
7	2000	45	M	CDX
8	7000	39	M	FLZ
9	12000	33	F	PTX
10	8000	32	F	FLZ

The groupby method allows us to group the rows of a DataFrame by value, with respect to a specified column. Suppose we want to group all rows that have the same value for sex:

df.groupby('sex')

<pandas.core.groupby.groupby.DataFrameGroupBy object at 0x0000029E02F239E8>

This operation returns an object of type DataFrameGroupby on which aggregate operations (e.g., sums and averages) can be performed. Let’s now assume we want to calculate the average of all values that fall into the same group (i.e., we calculate the average of the rows that have the same value for sex):

df.groupby('sex').mean()

	income	age
sex
F	8600.000000	28.400000
M	5333.333333	37.333333

If we are interested in only one of the variables, we can select it before or after the operation on the aggregated data:

df.groupby('sex')['age'].mean() #equivalently: df.groupby('sex').mean()['age']

sex
F    28.400000
M    37.333333
Name: age, dtype: float64

The table shows the average income and average age of male and female subjects. Since the mean operation can only be applied to numerical values, the Company column has been excluded. We can obtain a similar table showing the sum of incomes and the sum of ages by changing mean to sum:

df.groupby('sex').sum()

	income	age
sex
F	43000	142
M	32000	224

In general, it is possible to use various aggregate functions besides mean and sum. Some examples are min, max, std. Two particularly interesting functions to use in this context are count and describe. Specifically, count counts the number of relevant elements, while describe calculates various statistics of the relevant values. Let’s see two examples:

df.groupby('sex').count()

	income	age	company
sex
F	5	5	5
M	6	6	6

The number of elements is the same for the various columns as there are no NaN values in the DataFrame.

df.groupby('sex').describe()

	age								income
	count	mean	std	min	25%	50%	75%	max	count	mean	std	min	25%	50%	75%	max
sex
F	5.0	28.400000	6.268971	18.0	27.00	32.0	32.0	33.0	5.0	8600.000000	2880.972058	5000.0	7000.0	8000.0	11000.0	12000.0
M	6.0	37.333333	6.947422	28.0	32.75	37.0	43.5	45.0	6.0	5333.333333	3829.708431	1000.0	2250.0	5000.0	8500.0	10000.0

For each numerical variable (age and income), several statistics were calculated. Sometimes it can be clearer to visualize the transposed dataframe:

df.groupby('sex').describe().transpose()

	sex	F	M
age	count	5.000000	6.000000
	mean	28.400000	37.333333
	std	6.268971	6.947422
	min	18.000000	28.000000
	25%	27.000000	32.750000
	50%	32.000000	37.000000
	75%	32.000000	43.500000
	max	33.000000	45.000000
income	count	5.000000	6.000000
	mean	8600.000000	5333.333333
	std	2880.972058	3829.708431
	min	5000.000000	1000.000000
	25%	7000.000000	2250.000000
	50%	8000.000000	5000.000000
	75%	11000.000000	8500.000000
	max	12000.000000	10000.000000

This view allows us to compare different statistics of the two variables age and income for M and F.

Question 10

Considering the previously created DataFrame, use groupby to obtain the sum of the incomes of employees of a given company.

Crosstab#

Crosstabs allow for the description of relationships between two or more categorical variables. Once a pair of categorical variables is specified, the rows and columns of the crosstab (also known as a “contingency table”) independently enumerate all unique values of the two categorical variables, so that each cell of the crosstab identifies a specific pair of values. Within the cells, the numbers of elements for which the two categorical variables take on a specific pair of values are then reported.

Suppose we want to study the relationships between company and sex:

pd.crosstab(df['sex'],df['company'])

company	CDX	FLZ	PTX
sex
F	1	3	1
M	3	1	2

The table above tells us, for example, that in company CDX, \(1\) subject is female, while \(3\) subjects are male. Similarly, one subject from company FLZ is male, while three subjects are female. It is possible to obtain frequencies instead of counts, by using normalize=True:

pd.crosstab(df['sex'],df['company'], normalize=True)

company	CDX	FLZ	PTX
sex
F	0.090909	0.272727	0.090909
M	0.272727	0.090909	0.181818

Alternatively, we can normalize the table only by rows or only by columns by specifying normalize='index' or normalize='columns':

pd.crosstab(df['sex'],df['company'], normalize='index')

company	CDX	FLZ	PTX
sex
F	0.2	0.600000	0.200000
M	0.5	0.166667	0.333333

This table shows the percentages of people working in the three different companies for each gender, e.g., “20% of women work at CDX”. Similarly, we can normalize by columns as follows:

pd.crosstab(df['sex'],df['company'], normalize='columns')

company	CDX	FLZ	PTX
sex
F	0.25	0.75	0.333333
M	0.75	0.25	0.666667

This table shows the percentages of men and women working in each company, e.g., “25% of CDX workers are women”.

If we want to study the relationships between more than two categorical variables, we can specify a list of columns when building the crosstab:

pd.crosstab(df['sex'],[df['age'],df['company']])

age	18	27	28	32		33	35	39	45
company	CDX	FLZ	PTX	CDX	FLZ	PTX	CDX	FLZ	CDX	PTX
sex
F	1	1	0	0	2	1	0	0	0	0
M	0	0	1	1	0	0	1	1	1	1

Each cell of the crosstab above counts the number of observations reporting a specific triplet of values. For example, 1 subject is male, works for PTX, and is 28 years old, while 2 subjects are female, work for FLZ, and are 32 years old.

In addition to reporting counts and frequencies, a crosstab allows for the calculation of statistics for third variables considered non-categorical. Suppose we want to know the average age of people of a given sex working for a given company. We can build a crosstab by specifying a new variable (age) for values. Since some aggregate value needs to be calculated for this variable, we also need to specify aggfunc, for example, mean (to calculate the average of the relevant values):

pd.crosstab(df['sex'],df['company'], values=df['age'], aggfunc='mean')

company	CDX	FLZ	PTX
sex
F	18.000000	30.333333	33.0
M	37.333333	39.000000	36.5

The table tells us that the average age of male employees for CDX is \(37.33\) years.

Question 11

Construct a crosstab that, for each company, reports the number of employees of a given age.

“Explicit” Manipulation of DataFrames#

In some cases, it can be useful to treat DataFrames “explicitly” as matrices of values. Consider, for example, the following DataFrame:

df123 = pd.DataFrame({'Category':[1,2,3], 'NumberOfElements':[3,1,2]})
df123

	Category	NumberOfElements
0	1	3
1	2	1
2	3	2

Suppose we want to build a new DataFrame that, for each row of the df123 DataFrame, contains exactly “NumberOfElements” rows with the value of “NumberOfElements” equal to one. We essentially want to “expand” the DataFrame above as follows:

df123 = pd.DataFrame({'Category':[1,1,1,2,3,3], 'NumberOfElements':[1,1,1,1,1,1]})
df123

	Category	NumberOfElements
0	1	1
1	1	1
2	1	1
3	2	1
4	3	1
5	3	1

To do this automatically, we can treat the DataFrame “more explicitly” as a matrix of values by iterating through its rows. The new DataFrame will first be built as a list of Series (the rows of the DataFrame) and then transformed into a DataFrame:

newdat = []
for i, row in df123.iterrows(): # iterrows allows iterating over the rows of a DataFrame
    for j in range(row['NumberOfElements']):
        newrow = row.copy()
        newrow['NumberOfElements']=1
        newdat.append(newrow)
pd.DataFrame(newdat)

	Category	NumberOfElements
0	1	1
1	1	1
2	1	1
3	2	1
4	3	1
5	3	1

pd.DataFrame({'Category':[1,2,3], 'NumberOfElements':[3,5,3], 'CheckedElements':[1,2,1]})

	Category	NumberOfElements	CheckedElements
0	1	3	1
1	2	5	2
2	3	3	1

DataFrame Concatenation#

DataFrames can be concatenated by rows as shown below:

d1 = pd.DataFrame({'A':[1,2,3,4],'B':[3,2,6,7],'C':[0,2,-1,12]})
d2 = pd.DataFrame({'A':[92,8],'B':[44,-2],'C':[0,2]})
print(d1)
print(d2)

pd.concat([d1,d2])

	A	B	C
0	1	3	0
1	2	2	2
2	3	6	-1
3	4	7	12
0	92	44	0
1	8	-2	2

If the columns are not compatible, NaN will appear:

d1 = pd.DataFrame({'A':[1,2,3,4],'B':[3,2,6,7],'C':[0,2,-1,12]})
d2 = pd.DataFrame({'A':[92,8],'D':[0,2]})

pd.concat([d1,d2])

	A	B	C	D
0	1	3.0	0.0	NaN
1	2	2.0	2.0	NaN
2	3	6.0	-1.0	NaN
3	4	7.0	12.0	NaN
0	92	NaN	NaN	0.0
1	8	NaN	NaN	2.0

Concatenation can also occur by columns:

d1 = pd.DataFrame({'A':[1,2],'B':[3,7],'C':[-1,12]})
d2 = pd.DataFrame({'A':[92,8],'D':[0,2]})

pd.concat([d1,d2], axis=1)

	A	B	C	A	D
0	1	3	-1	92	0
1	2	7	12	8	2

DataFrame Merge#

Two DataFrames can be merged using a merge operation similar to what happens in databases. Let’s consider two example dataframes:

a = pd.DataFrame({'key': ['k0', 'k1', 'k2'],
                     'a': ['v1', 'v2', 'v3'],
                     'b': ['v4', 'v5', 'v6'],
                     'c': ['v7', 'v8', 'v9']})
   
a

	key	a	b	c
0	k0	v1	v4	v7
1	k1	v2	v5	v8
2	k2	v3	v6	v9

b = pd.DataFrame({'key': ['k0', 'k1', 'k2'],
                     'd': ['v9', 'v11', 'v12'],
                     'e': ['v13', 'v4', 'v5']})
b

	key	d	e
0	k0	v9	v13
1	k1	v11	v4
2	k2	v12	v5

The two dataframes have one column in common that acts as a key and other columns that act as values. The merge operation allows to combine the dataframes based on the keys:

pd.merge(a,b,on='key')

	key	a	b	c	d	e
0	k0	v1	v4	v7	v9	v13
1	k1	v2	v5	v8	v11	v4
2	k2	v3	v6	v9	v12	v5

DataFrame Joins#

join operations can be applied to combine dataframes with compatible indices:

a = pd.DataFrame({'a': ['v1', 'v2', 'v3'],
                     'b': ['v4', 'v5', 'v6'],
                     'c': ['v7', 'v8', 'v9']},
                     index = ['k0', 'k1', 'k2'])
   
a

	a	b	c
k0	v1	v4	v7
k1	v2	v5	v8
k2	v3	v6	v9

b = pd.DataFrame({'d': ['v9', 'v11', 'v12'],
                     'e': ['v13', 'v4', 'v5']},
                     index = ['k0', 'k3', 'k2'],)
b

	d	e
k0	v9	v13
k3	v11	v4
k2	v12	v5

a.join(b)

	a	b	c	d	e
k0	v1	v4	v7	v9	v13
k1	v2	v5	v8	NaN	NaN
k2	v3	v6	v9	v12	v5

As can be seen, the join operation only occurs by using the common indexes.

Input/Output#

Pandas provides several functions for reading and writing data. We will specifically look at the functions for reading and writing csv files. It is possible to read csv files (https://it.wikipedia.org/wiki/Comma-separated_values) using the pd.read_csv function. Reading can be done from local files by passing the relative path or from URLs:

data=pd.read_csv('http://iplab.dmi.unict.it/furnari/downloads/students.csv')
data.head()

	admit	gre	gpa	prestige
0	0	380	3.61	3
1	1	660	3.67	3
2	1	800	4.00	1
3	1	640	3.19	4
4	0	520	2.93	4

Likewise, you can write a DataFrame to a CSV file as follows:

data.to_csv('file.csv')

Since indices may not be sequential in a DataFrame, Pandas inserts them into the csv as an “unnamed column”. For example, the first few lines of the file we just wrote (file.csv) are as follows:

,admit,gre,gpa,prestige
0,0,380,3.61,3
1,1,660,3.67,3
2,1,800,4.0,1
3,1,640,3.19,4
4,0,520,2.93,4

As you can see, the first column contains the index values, but it has no name. This can cause problems when we reload the DataFrame:

data=pd.read_csv('file.csv')
data.head()

	Unnamed: 0	admit	gre	gpa	prestige
0	0	0	380	3.61	3
1	1	1	660	3.67	3
2	2	1	800	4.00	1
3	3	1	640	3.19	4
4	4	0	520	2.93	4

We can solve the problem in several ways:

Eliminate the “Unnamed: 0” column from the newly loaded DataFrame (only if the indices are sequential);
Specify to use the “Unnamed: 0” column as the index column during loading;
Save the DataFrame without indices (only if the indices are sequential).

Let’s look at the three cases:

data=pd.read_csv('file.csv')
data.drop('Unnamed: 0', axis=1).head()

	admit	gre	gpa	prestige
0	0	380	3.61	3
1	1	660	3.67	3
2	1	800	4.00	1
3	1	640	3.19	4
4	0	520	2.93	4

data=pd.read_csv('file.csv', index_col='Unnamed: 0')
data.head()

	admit	gre	gpa	prestige
0	0	380	3.61	3
1	1	660	3.67	3
2	1	800	4.00	1
3	1	640	3.19	4
4	0	520	2.93	4

data.to_csv('file.csv', index=False)
pd.read_csv('file.csv').head()

	admit	gre	gpa	prestige
0	0	380	3.61	3
1	1	660	3.67	3
2	1	800	4.00	1
3	1	640	3.19	4
4	0	520	2.93	4

Data Manipulation Example#

Often, data needs to be properly processed to be analyzed. Let’s look at an example of how to combine the tools discussed above to manipulate a real dataset.

We will consider the dataset available at this URL: https://www.kaggle.com/lava18/google-play-store-apps. A copy of the dataset is available at the following URL for educational purposes: http://iplab.dmi.unict.it/furnari/downloads/googleplaystore.csv. Let’s load the dataset and display the first few rows to ensure it has been loaded correctly:

data = pd.read_csv('http://iplab.dmi.unict.it/furnari/downloads/googleplaystore.csv')
data.head()

	App	Category	Rating	Reviews	Size	Installs	Type	Content Rating	Genres	Last Updated	Current Ver	Android Ver
0	Photo Editor & Candy Camera & Grid & ScrapBook	ART_AND_DESIGN	4.1	159	19M	10,000+	Free	Everyone	Art & Design	January 7, 2018	1.0.0	4.0.3 and up
1	Coloring book moana	ART_AND_DESIGN	3.9	967	14M	500,000+	Free	Everyone	Art & Design;Pretend Play	January 15, 2018	2.0.0	4.0.3 and up
2	U Launcher Lite – FREE Live Cool Themes, Hide ...	ART_AND_DESIGN	4.7	87510	8.7M	5,000,000+	Free	Everyone	Art & Design	August 1, 2018	1.2.4	4.0.3 and up
3	Sketch - Draw & Paint	ART_AND_DESIGN	4.5	215644	25M	50,000,000+	Free	Teen	Art & Design	June 8, 2018	Varies with device	4.2 and up
4	Pixel Draw - Number Art Coloring Book	ART_AND_DESIGN	4.3	967	2.8M	100,000+	Free	Everyone	Art & Design;Creativity	June 20, 2018	1.1	4.4 and up

Display the dataset properties:

data.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 10841 entries, 0 to 10840
Data columns (total 13 columns):
App               10841 non-null object
Category          10841 non-null object
Rating            9367 non-null float64
Reviews           10841 non-null object
Size              10841 non-null object
Installs          10841 non-null object
Type              10840 non-null object
Price             10841 non-null object
Content Rating    10840 non-null object
Genres            10841 non-null object
Last Updated      10841 non-null object
Current Ver       10833 non-null object
Android Ver       10838 non-null object
dtypes: float64(1), object(12)
memory usage: 1.1+ MB

The dataset contains \(10841\) observations and \(13\) variables. We observe that many of the variables (except “Rating”) are of type “object”, even though they represent numerical values (e.g., Reviews, Size, Installs, and Price). Observing the first rows of the DataFrame displayed above, we can deduce that:

Size is not represented as a numerical value as it contains the unit of measurement “M”;
Installs is actually a categorical variable (it has a “+” at the end, thus indicating the “more than xxxx installations” class);

There are no apparent reasons why Reviews and Rating were not interpreted as numbers. Let’s build a filter function that identifies whether a value is convertible to a given type or not:

def cannot_convert(x, t=float):
    try:
        t(x)
        return False
    except:
        return True
print(cannot_convert('12'))
print(cannot_convert('12f'))

False
True

We apply the filter to the Review column to display values that cannot be converted:

list(filter(cannot_convert,data['Reviews']))

['3.0M']

We can replace this value with its full version using the replace method:

data['Reviews']=data['Reviews'].replace({'3.0M':3000000})

At this point, we can convert the column’s value types to integers:

data['Reviews']=data['Reviews'].astype(int)

Let’s visualize the DataFrame information again:

data.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 10841 entries, 0 to 10840
Data columns (total 13 columns):
App               10841 non-null object
Category          10841 non-null object
Rating            9367 non-null float64
Reviews           10841 non-null int32
Size              10841 non-null object
Installs          10841 non-null object
Type              10840 non-null object
Price             10841 non-null object
Content Rating    10840 non-null object
Genres            10841 non-null object
Last Updated      10841 non-null object
Current Ver       10833 non-null object
Android Ver       10838 non-null object
dtypes: float64(1), int32(1), object(11)
memory usage: 1.0+ MB

Reviews is now a whole. We perform a similar analysis on the Price variable:

list(filter(cannot_convert, data['Price']))[:10] #display only the first 10 elements

['$4.99',
 '$4.99',
 '$4.99',
 '$4.99',
 '$3.99',
 '$3.99',
 '$6.99',
 '$1.49',
 '$2.99',
 '$3.99']

We can convert strings to float by removing the initial dollar using apply:

def strip_dollar(x):
    if x[0]=='$':
        return x[1:]
    else:
        return x
data['Price']=data['Price'].apply(strip_dollar)

Let’s see if there are any values that cannot be converted:

list(filter(cannot_convert, data['Price']))

['Everyone']

Since we don’t know how to interpret the value “Everyone”, let’s replace it with a NaN:

data['Price']=data['Price'].replace({'Everyone':np.nan})

Now we can proceed with the conversion:

data['Price'] = data['Price'].astype(float)
data.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 10841 entries, 0 to 10840
Data columns (total 13 columns):
App               10841 non-null object
Category          10841 non-null object
Rating            9367 non-null float64
Reviews           10841 non-null int32
Size              10841 non-null object
Installs          10841 non-null object
Type              10840 non-null object
Price             10840 non-null float64
Content Rating    10840 non-null object
Genres            10841 non-null object
Last Updated      10841 non-null object
Current Ver       10833 non-null object
Android Ver       10838 non-null object
dtypes: float64(2), int32(1), object(10)
memory usage: 1.0+ MB

We also modify “Size” by removing the final “M”:

data['Size']=data['Size'].apply(lambda x : x[:-1])

We verify the existence of non-convertible values:

list(filter(cannot_convert,data['Size']))[:10]

['Varies with devic',
 'Varies with devic',
 'Varies with devic',
 'Varies with devic',
 'Varies with devic',
 'Varies with devic',
 'Varies with devic',
 'Varies with devic',
 'Varies with devic',
 'Varies with devic']

We replace these values with NaN:

data['Size']=data['Size'].replace({'Varies with device':np.nan})

Let’s re-check for values that cannot be converted:

list(filter(cannot_convert, data['Size']))

['1,000']

We can remove the comma used to indicate thousands and convert to float:

data['Size']=data['Size'].apply(lambda x: float(str(x).replace(',','')))

data.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 10841 entries, 0 to 10840
Data columns (total 13 columns):
App               10841 non-null object
Category          10841 non-null object
Rating            9367 non-null float64
Reviews           10841 non-null int32
Size              9146 non-null float64
Installs          10841 non-null object
Type              10840 non-null object
Price             10840 non-null float64
Content Rating    10840 non-null object
Genres            10841 non-null object
Last Updated      10841 non-null object
Current Ver       10833 non-null object
Android Ver       10838 non-null object
dtypes: float64(3), int32(1), object(9)
memory usage: 1.0+ MB

Let’s evaluate whether it’s appropriate to also transform “Installs” into a numerical value. Let’s see how many unique values of “Installs” there are in the dataset:

data['Installs'].nunique()

We only have \(22\) values, which compared to the 10841 observations, indicate that “Installs” is a highly quantized variable, so it probably makes sense to consider it as categorical, rather than a numerical value.

The DataFrame contains NaN values. Depending on the case, it can make sense to keep them or remove them. Since there are many data points, we can remove them with dropna:

data=data.dropna()

We can therefore start exploring the data with the tools we’ve seen. Let’s visualize, for example, the average values of the numerical variables by category:

data.groupby('Category').mean()

	Rating	Reviews	Size	Price
Category
ART_AND_DESIGN	4.381034	1.874517e+04	12.939655	0.102931
AUTO_AND_VEHICLES	4.147619	1.575057e+04	24.728571	0.000000
BEAUTY	4.291892	5.020243e+03	15.513514	0.000000
BOOKS_AND_REFERENCE	4.320139	2.815291e+04	23.543750	0.145069
BUSINESS	4.119919	2.497765e+04	26.217480	0.249593
COMICS	4.130612	1.254822e+04	34.626531	0.000000
COMMUNICATION	4.102844	5.549962e+05	60.765403	0.197773
DATING	3.957803	2.254489e+04	18.312717	0.086590
EDUCATION	4.387273	6.435159e+04	30.588182	0.163273
ENTERTAINMENT	4.146667	1.621530e+05	21.853333	0.033222
EVENTS	4.478947	3.321605e+03	23.213158	0.000000
FAMILY	4.190347	1.801297e+05	37.459963	1.390074
FINANCE	4.112030	3.903023e+04	31.249624	9.172444
FOOD_AND_DRINK	4.097619	5.103793e+04	24.163095	0.059405
GAME	4.269507	1.386276e+06	46.827823	0.281704
HEALTH_AND_FITNESS	4.223767	4.519072e+04	29.658296	0.154350
HOUSE_AND_HOME	4.162500	2.935998e+04	17.505357	0.000000
LIBRARIES_AND_DEMO	4.204918	1.632359e+04	225.267213	0.000000
LIFESTYLE	4.093571	3.109027e+04	28.650714	6.976429
MAPS_AND_NAVIGATION	4.013684	3.858909e+04	26.282105	0.157474
MEDICAL	4.184259	4.392454e+03	49.643827	3.077901
NEWS_AND_MAGAZINES	4.143787	5.826802e+04	14.948521	0.023550
PARENTING	4.347727	1.999950e+04	21.579545	0.113409
PERSONALIZATION	4.323381	1.257211e+05	50.115827	0.427338
PHOTOGRAPHY	4.147034	3.260313e+05	18.970763	0.331992
PRODUCTIVITY	4.143830	1.854692e+05	38.899149	0.225362
SHOPPING	4.227933	2.624461e+05	33.397207	0.030615
SOCIAL	4.257062	1.830882e+05	24.317514	0.011186
SPORTS	4.204858	2.128411e+05	30.159109	0.324818
TOOLS	4.010742	1.663130e+05	47.929068	0.290047
TRAVEL_AND_LOCAL	4.043125	4.824554e+04	25.357500	0.165687
VIDEO_PLAYERS	4.025862	2.074172e+05	22.881897	0.008534
WEATHER	4.241176	7.639225e+04	24.805882	0.459608

Question 12

Display the average number of reviews per type (variable Type).

Exercises#

Exercise 1

Define a 3x4 matrix, then:

Print the first row of the matrix;

Print the second column of the matrix;

Sum the first and last columns of the matrix;

Sum the elements along the main diagonal;

Print the number of elements in the matrix.

Exercise 2

Generate an array of \(100\) numbers between \(2\) and \(4\) and calculate the sum of the elements whose squares have a value greater than \(8\).

Exercise 3

Generate the following matrix writing the smallest amount of code possible:
0 1 2
3 4 5
6 7 8
Repeat the exercise generating a \(25 \times 13\) matrix of the same type.

Exercise 4

Write the code to obtain this diagram:

Exercise 5

Load the dataset available at the following URL: https://raw.githubusercontent.com/agconti/kaggle-titanic/master/data/train.csv so as to use the values of the “PassengerId” column as indices and apply the following transformations:

Remove rows containing NaN values;

Modify the DataFrame by replacing every occurrence of “male” with “M” and every occurrence of “female” with “F” in the “Sex” column;

Insert a new column “Old” with a value of “1” if Age is greater than the average age of passengers and “0” otherwise;

Convert the values in the “Age” column to integers.

Exercise 6

Consider the dataset loaded and modified in the previous exercise. Find the name of the passenger with ticket code “345779”.

Exercise 7

What are the names of the 5 youngest passengers?

Exercise 8

Consider the dataset loaded and modified in the previous exercise. Select all observations relating to passengers between 20 and 30 years of age.

Exercise 9

Consider the dataset loaded and modified in the previous exercises. Calculate the average fare paid by female passengers in second class.

Exercise 10

Consider the dataset loaded and modified in the previous exercises. Construct a crosstab to answer the following questions:

How many male passengers survived?

How many female passengers did not survive?

Exercise 11

Consider the dataset loaded and modified in the previous exercises. Construct a crosstab that allows you to answer the following questions:

How many male passengers survived in first class?

How many female passengers survived in third class?

How many male passengers survived in third class?

Exercise 12

Consider the following DataFrame:
pd.DataFrame({'Category':[1,2,3], 'NumberOfElements':[3,2,3], 'CheckedElements':[1,2,1]})
Construct a new DataFrame that contains the same columns as the considered DataFrame and that for each row of it contains NumberOfElements new rows with category equal to Category of which CheckedElements with value of CheckedElements equal to one and the rest with value of CheckedElements equal to zero.

The result of the manipulation should be equal to the following dataset:
pd.DataFrame({'Category':[1,1,1,2,2,3,3,3], 
              'NumberOfElements':[1,1,1,1,1,1,1,1], 
              'CheckedElements':[1,0,0,1,1,1,0,0]})

References#

Pandas Documentation: https://pandas.pydata.org/pandas-docs/stable/
Kaggle Website (where to find data to analyze): http://kaggle.com/
Page from which to download various CSV datasets from the R library: https://vincentarelbundock.github.io/Rdatasets/datasets.html