14. Laboratorio su Misure di Tendenza Centrale, Dispersione e Forma#
Per esaminare gli strumenti in oggetto, ci avvremo del dataset Titanic. Si tratta di un dataset classico, che riporta alcune informazioni, quali sesso, età, classe di imbarco e sopravvivenza di alcuni passaggeri del Titanic. Troviamo una versione del dataset al seguente URL:
https://raw.githubusercontent.com/agconti/kaggle-titanic/master/data/train.csv
Carichiamo il dataset mediante la libreria Pandas:
import pandas as pd
titanic = pd.read_csv('https://raw.githubusercontent.com/agconti/kaggle-titanic/master/data/train.csv',
index_col='PassengerId')
Visualizziamo alcune informazioni sul dataset:
titanic.info()
<class 'pandas.core.frame.DataFrame'>
Int64Index: 891 entries, 1 to 891
Data columns (total 11 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Survived 891 non-null int64
1 Pclass 891 non-null int64
2 Name 891 non-null object
3 Sex 891 non-null object
4 Age 714 non-null float64
5 SibSp 891 non-null int64
6 Parch 891 non-null int64
7 Ticket 891 non-null object
8 Fare 891 non-null float64
9 Cabin 204 non-null object
10 Embarked 889 non-null object
dtypes: float64(2), int64(4), object(5)
memory usage: 83.5+ KB
Il dataset contiene \(891\) osservazioni e \(11\) colonne. Visualizziamo le prime righe del DataFrame per vedere com’è organizzato:
titanic.head()
| Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| PassengerId | |||||||||||
| 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S |
| 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th... | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S |
| 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 5 | 0 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.0500 | NaN | S |
14.1. Numerosità#
La numerosità dei campioni costituiti dalle singole colonne può essere ottenuta mediante il metodo len:
print(len(titanic['Age']))
891
Il metodo len però non considera i dati incompleti (la colonna potrebbe contenere dei NaN). Per ottenere un conteggio più corretto possiamo esplicitamente eliminare i NaN con dropna:
print(len(titanic['Age'].dropna()))
714
Come possiamo notare, il campione è meno numeroso di quello che sembrava. Alternativamente possiamo richiamare info sul DataFrame:
titanic.info()
<class 'pandas.core.frame.DataFrame'>
Int64Index: 891 entries, 1 to 891
Data columns (total 11 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Survived 891 non-null int64
1 Pclass 891 non-null int64
2 Name 891 non-null object
3 Sex 891 non-null object
4 Age 714 non-null float64
5 SibSp 891 non-null int64
6 Parch 891 non-null int64
7 Ticket 891 non-null object
8 Fare 891 non-null float64
9 Cabin 204 non-null object
10 Embarked 889 non-null object
dtypes: float64(2), int64(4), object(5)
memory usage: 83.5+ KB
Lo schema sopra mostra il numero di oggetti non-null per ogni colonna. Coerentemente con quanto visto prima, abbiamo solo \(714\) elementi di Age validi.
Domanda 1
Qual è la numerosità di
Cabin?
14.2. Indicatori Centrali: Media, Mediana e Moda#
14.2.1. Media#
Possiamo calcolarlo manualmente la media come segue
titanic['Age'].sum()/len(titanic['Age'].dropna())
29.69911764705882
O semplicemente mediante la funzione mean:
titanic['Age'].mean()
29.69911764705882
Domanda 2
In quali casi la media riassume bene i dati? In quali casi no?
14.2.2. Mediana#
Possiamo calcolare la mediana manualmente come segue:
import numpy as np
a=pd.Series([1,-2,3,-4,7])
print(a.sort_values())
print("Mediana: {}".format(a.sort_values().iloc[2]))
3 -4
1 -2
0 1
2 3
4 7
dtype: int64
Mediana: 1
o alternativamente mediante il metodo median:
a.median()
1.0
Calcoliamo ad esempio il valore mediano di Age:
titanic['Age'].median()
28.0
Domanda 3
Si confronti la media di
Agecon la sua mediana. I due valori corrispondono? Perché? Quali dei due valori è uguale a uno dei valori appartenente al campione?
14.2.3. Quantili, Percentili e Quartili#
In pandas, i quantili si ottengono mediante il metodo quantile:
print("Quantile di ordine 0 (minimo):", titanic['Age'].quantile(0))
print("Quantile di ordine 0.5 (mediana):", titanic['Age'].quantile(0.5))
print("Quantile di ordine 1 (massimo):", titanic['Age'].quantile(1))
print("Quantile di ordine 0.15:", titanic['Age'].quantile(0.15))
Quantile di ordine 0 (minimo): 0.42
Quantile di ordine 0.5 (mediana): 28.0
Quantile di ordine 1 (massimo): 80.0
Quantile di ordine 0.15: 17.0
I percentili si ottengono sempre mediante la funzione quantile, dividendo l’ordine per percentile per 100:
print("Percentile di ordine 50% (mediana):", titanic['Age'].quantile(50/100))
print("Percentile di ordine 30%:", titanic['Age'].quantile(30/100))
Percentile di ordine 50% (mediana): 28.0
Percentile di ordine 30%: 22.0
Analogamente, i quartili si ottengono dividendo l’ordine del quartile per 4:
print("Quartile di ordine 0 (minimo):", titanic['Age'].quantile(0/4))
print("Quartile di ordine 1:", titanic['Age'].quantile(1/4))
print("Quartile di ordine 2 (mediana):", titanic['Age'].quantile(2/4))
print("Quartile di ordine 3:", titanic['Age'].quantile(3/4))
print("Quartile di ordine 4 (massimo):", titanic['Age'].quantile(4/4))
Quartile di ordine 0 (minimo): 0.42
Quartile di ordine 1: 20.125
Quartile di ordine 2 (mediana): 28.0
Quartile di ordine 3: 38.0
Quartile di ordine 4 (massimo): 80.0
Domanda 4
Anche i quartili, come il minimo e il massimo, permettono di farsi un’idea dell’ordine di grandezza dei dati analizzati, tuttavia, i quartili hanno un vantaggio, quale?
14.2.4. Moda#
Possiamo calcolare la moda manualmente come segue:
print(titanic['Age'].value_counts().head())
print("Moda: ",titanic['Age'].value_counts().index[0])
24.0 30
22.0 27
18.0 26
19.0 25
28.0 25
Name: Age, dtype: int64
Moda: 24.0
Alternativamente, possiamo usare la funzione mode:
titanic['Age'].mode()
0 24.0
Name: Age, dtype: float64
Domanda 5
Si confrontino la moda di
Agecon la sua media. I valori corrispondono? Perché?
14.3. Indicatori di dispersione#
14.3.1. Minimo, Massimo e Range#
Massimo, minimo e range vengono calcolati semplicemente come segue:
print("Minimo:", titanic['Age'].min())
print("Massimo:", titanic['Age'].max())
print("Range:", titanic['Age'].max() - titanic['Age'].min())
Minimo: 0.42
Massimo: 80.0
Range: 79.58
Domanda 6
Il range è un indicatore di dispersione robusto alla presenza di “outliers”?
14.3.2. Distanza interquartile#
Possiamo calcolare la distanza interquartile come segue:
q11,q13 = titanic[titanic['Sex']=='male']['Age'].quantile([1/4,3/4])
q21,q23 = titanic[titanic['Sex']=='female']['Age'].quantile([1/4,3/4])
print("Lo scarto interquartile di sample 1 è:",q13-q11)
print("Lo scarto interquartile di sample 2 è:",q23-q21)
Lo scarto interquartile di sample 1 è: 18.0
Lo scarto interquartile di sample 2 è: 19.0
Domanda 7
La distanza interquartile è sempre una misura di dispersione robusta? Cosa succede nel caso di distribuzioni fortemente asimmetriche?
14.3.3. Varianza e Deviazione Standard#
La varianza può essere calcolata richiamando il metodo var:
print(titanic[titanic['Sex']=='male']['Age'].var())
print(titanic[titanic['Sex']=='female']['Age'].var())
215.44957942429036
199.0962330533453
La deviazione standard si calcola mediante il metodo std:
print("Deviazione standard del campione:",titanic['Age'].std(),"anni")
Deviazione standard del campione: 14.526497332334044 anni
La deviazione standard ci dice qualcosa anche sulla “forma” della distribuzione. Confrontiamo ad esempio le deviazioni standard delle età dei passeggeri appartenenti alle tre classi di imbarco:
titanic.groupby('Pclass')['Age'].std()
Pclass
1 14.802856
2 14.001077
3 12.495398
Name: Age, dtype: float64
Confrontiamo adesso le densità stimate dai tre campioni:
from matplotlib import pyplot as plt
titanic.groupby('Pclass')['Age'].plot.density(figsize=(8,4))
plt.grid()
plt.legend()
plt.show()
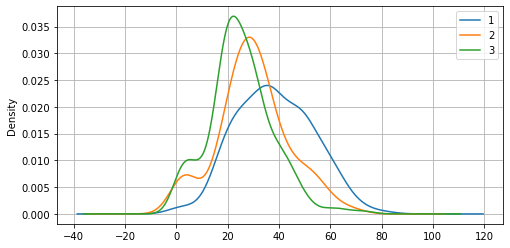
Domanda 8
Esiste una relazione tra le deviazioni standard dei campioni e le relative densità? Quale?
14.3.3.1. Normalizzazione tra 0 e 1#
Secondo la normalizzazione tra 0 e 1, i dati vengono riscalati come segue:
Possiamo effettuare questa trasformazione in Pandas come segue:
age_norm_01 = (titanic['Age']-titanic['Age'].min())/(titanic['Age'].max()-titanic['Age'].min())
Verifichiamo che gli estremi del nuovo campione siano 0 e 1:
print(age_norm_01.min(), age_norm_01.max())
0.0 1.0
14.3.3.2. Normalizzazione tra -1 e 1#
I dati vengono riscalati come segue:
Possiamo effettuare questa trasformazione in Pandas come segue:
age_norm_11 = (titanic['Age'].max()+titanic['Age'].min()-2*titanic['Age'])/(titanic['Age'].max()-titanic['Age'].min())
Verifichiamo che gli estremi del nuovo campione siano -1 e 1:
print(age_norm_11.min(), age_norm_11.max())
-1.0 1.0
14.3.4. Standardizzazione (z-scoring)#
Possiamo effettuare questa normalizzazione usando la funzione zscore di scipy:
from scipy.stats import zscore
zscore([0,1,2,3,4])
array([-1.41421356, -0.70710678, 0. , 0.70710678, 1.41421356])
Applichiamo questa normalizzazione alle età dei passeggeri del Titanic:
age_z=zscore(titanic['Age'].dropna())
plt.figure(figsize=(12,4))
plt.subplot(121)
titanic['Age'].plot.density()
plt.grid()
plt.subplot(122)
age_z.plot.density()
plt.grid()
plt.show()
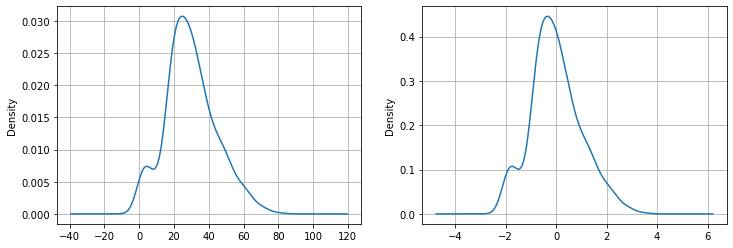
14.3.5. Indicatori di Forma#
14.3.5.1. Asimmetria (skewness)#
Posso calcolare il valore di skewness mediante il metodo di Pandas skew. Vediamo un paio di esempi sul dataset di pesi e altezze:
titanic.skew()
/var/folders/cs/p62_d78d49n3ddj0xlfh1h7r0000gn/T/ipykernel_31494/1596635564.py:1: FutureWarning: Dropping of nuisance columns in DataFrame reductions (with 'numeric_only=None') is deprecated; in a future version this will raise TypeError. Select only valid columns before calling the reduction.
titanic.skew()
Survived 0.478523
Pclass -0.630548
Age 0.389108
SibSp 3.695352
Parch 2.749117
Fare 4.787317
dtype: float64
Confrontiamo i risultati con le stime di densità:
titanic.plot.density(subplots=True, layout=(2,3), figsize=(12,8), sharex=False)
array([[<AxesSubplot:ylabel='Density'>, <AxesSubplot:ylabel='Density'>,
<AxesSubplot:ylabel='Density'>],
[<AxesSubplot:ylabel='Density'>, <AxesSubplot:ylabel='Density'>,
<AxesSubplot:ylabel='Density'>]], dtype=object)
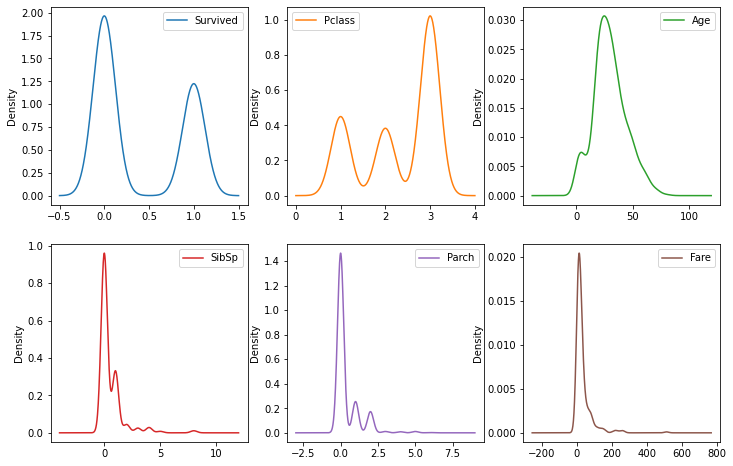
I valori di skewness di pesi e altezze sarnno:
import pandas as pd
hw=pd.read_csv('http://antoninofurnari.it/downloads/height_weight.csv')
print(f"Skweness pesi: {hw['weight'].skew():0.2f}")
print(f"Skweness altezza: {hw['height'].skew():0.2f}")
Skweness pesi: 0.57
Skweness altezza: 0.19
Confrontando con le densità:
hw.plot.density(subplots=True, layout=(2,3), figsize=(12,8), sharex=False)
array([[<AxesSubplot:ylabel='Density'>, <AxesSubplot:ylabel='Density'>,
<AxesSubplot:ylabel='Density'>],
[<AxesSubplot:ylabel='Density'>, <AxesSubplot:ylabel='Density'>,
<AxesSubplot:ylabel='Density'>]], dtype=object)
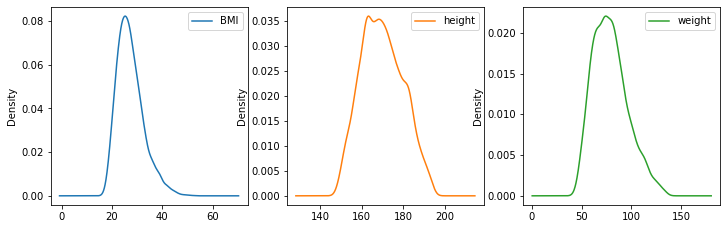
14.3.5.2. Curtosi (kurtosis)#
Analogamente, possiamo calcolare la curtosi con il metodo Kurtosis:
titanic.kurtosis()
/var/folders/cs/p62_d78d49n3ddj0xlfh1h7r0000gn/T/ipykernel_31494/3071249296.py:1: FutureWarning: Dropping of nuisance columns in DataFrame reductions (with 'numeric_only=None') is deprecated; in a future version this will raise TypeError. Select only valid columns before calling the reduction.
titanic.kurtosis()
Survived -1.775005
Pclass -1.280015
Age 0.178274
SibSp 17.880420
Parch 9.778125
Fare 33.398141
dtype: float64
hw.kurtosis()
/var/folders/cs/p62_d78d49n3ddj0xlfh1h7r0000gn/T/ipykernel_31494/4227707798.py:1: FutureWarning: Dropping of nuisance columns in DataFrame reductions (with 'numeric_only=None') is deprecated; in a future version this will raise TypeError. Select only valid columns before calling the reduction.
hw.kurtosis()
BMI 0.917179
height -0.687287
weight -0.056386
dtype: float64
14.4. Boxplot#
Possiamo visualizzare un boxplot direttamente mediante Pandas:
from matplotlib import pyplot as plt
titanic['Age'].plot.box(figsize=(2,6))
plt.grid()
plt.show()
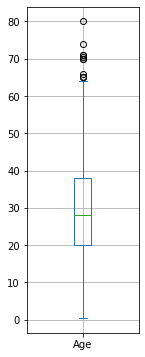
Alternativamente, possiamo mostrare un boxplot mediante matplotlib:
plt.figure(figsize=(2,6))
plt.boxplot(titanic['Age'].dropna())#inseriamo dropna per eliminare i NaN
plt.grid()
plt.show()
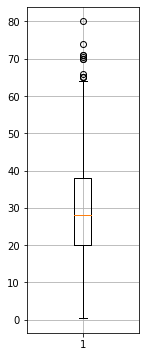
14.4.1. Boxplot Multipli#
Mediante Pandas è possibile mostrare i boxplot di tutte le variabili numeriche di un DataFrame come segue:
titanic.plot.box()
plt.grid()
plt.show()
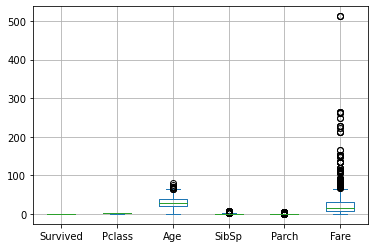
Se vogliamo restringere l’analisi ad alcune variabili, possiamo selezionare solo le variabili interessate come segue:
titanic[['Age','Fare']].plot.box()
plt.grid()
plt.show()
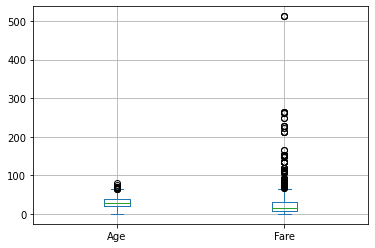
E’ inoltre possibile confrontare i boxplot di diversi campioni. Supponiamo di voler confrontare le età di uomini e donne:
titanic.boxplot(by='Sex',column=['Age'], figsize=(8,6))
plt.show()
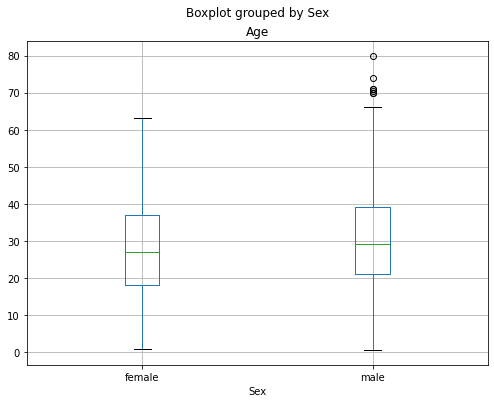
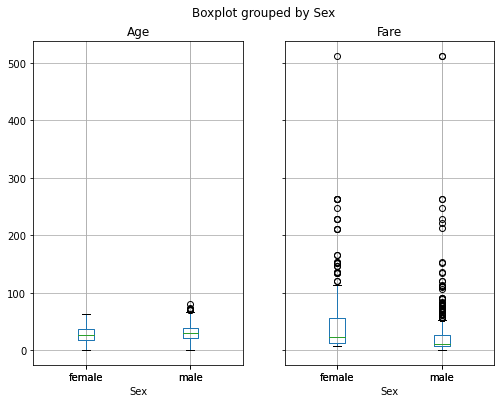
Nel caso di variabili multiple:
titanic.boxplot(by='Sex',column=['Age','Fare'], figsize=(8,6))
plt.show()
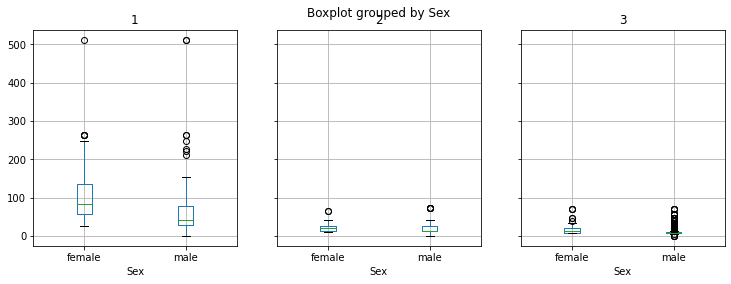
Possiamo anche combinare i boxplot con un groupby. Confrontiamo ad esempio le tariffe pagate da e donne appartenenti alle tre classi di imbarco:
titanic.groupby('Pclass').boxplot(by='Sex',column=['Fare'], figsize=(12,4), layout=(1,3))
plt.show()
titanic.groupby('Pclass').boxplot(by='Sex',column=['Age'], figsize=(12,4), layout=(1,3))
plt.show()
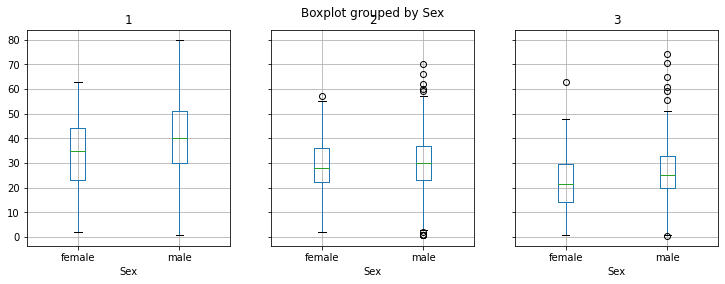
Domanda 9
Si confrontino le età di donne e uomini nelle varie classi di imbarco. In quale classe esistano differenze notevoli tra le età di uomini e donne?
14.5. Esercizi#
Esercizio 1
Considerando il dataset Titanic, si calcolino per ogni variabile la numerosità, la media, la deviazione standard, il minimo, il massimo, il valore mediano, il primo e il terzo quartile. Dopo aver calcolato i valori richiesti individualmente, si utilizzi il metodo
describeper ottenere tali valori. Qual è la variabile più dispersa?
Esercizio 2
Considerando il dataset Titanic, per ognuna delle tre classi, si calcolino medie e varianze delle età dei passeggeri. In quale classe le età sono meno disperse? Quale classe contiene i soggetti più giovani? Si completi l’analisi con dei grafici a barre.

