22. Laboratorio su regressione logistica#
Supponiamo di voler studiare la correlazione tra due variabili, di cui una (la variabile dipendente) sia categorica e binaria (ovvero, che può assumere solo i valori \(0\) e \(1\)). Per studiare questo caso, considereremo un esempio riadattato da http://nbviewer.jupyter.org/github/justmarkham/DAT8/blob/master/notebooks/12_logistic_regression.ipynb.
Consideriamo il Glass Identification Data Set (https://archive.ics.uci.edu/ml/datasets/glass+identification). Si tratta di un dataset che contiene una serie di misurazioni per diversi campioni di vetro. Carichiamo il dataset mediante la API di UCI ML:
from ucimlrepo import fetch_ucirepo
# fetch dataset
glass_identification = fetch_ucirepo(id=42)
# data (as pandas dataframes)
X = glass_identification.data.features
y = glass_identification.data.targets
glass= X.join(y)
glass.info()
glass.head()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 214 entries, 0 to 213
Data columns (total 10 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 RI 214 non-null float64
1 Na 214 non-null float64
2 Mg 214 non-null float64
3 Al 214 non-null float64
4 Si 214 non-null float64
5 K 214 non-null float64
6 Ca 214 non-null float64
7 Ba 214 non-null float64
8 Fe 214 non-null float64
9 Type_of_glass 214 non-null int64
dtypes: float64(9), int64(1)
memory usage: 16.8 KB
| RI | Na | Mg | Al | Si | K | Ca | Ba | Fe | Type_of_glass | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.52101 | 13.64 | 4.49 | 1.10 | 71.78 | 0.06 | 8.75 | 0.0 | 0.0 | 1 |
| 1 | 1.51761 | 13.89 | 3.60 | 1.36 | 72.73 | 0.48 | 7.83 | 0.0 | 0.0 | 1 |
| 2 | 1.51618 | 13.53 | 3.55 | 1.54 | 72.99 | 0.39 | 7.78 | 0.0 | 0.0 | 1 |
| 3 | 1.51766 | 13.21 | 3.69 | 1.29 | 72.61 | 0.57 | 8.22 | 0.0 | 0.0 | 1 |
| 4 | 1.51742 | 13.27 | 3.62 | 1.24 | 73.08 | 0.55 | 8.07 | 0.0 | 0.0 | 1 |
Il dataset contiene \(214\) osservazioni e \(10\) colonne. I significati delle variabili sono i seguenti:
id: l’id della riga del DataFrame;
ri: indice di rifrazione del vetro;
na: percentuale di sodio;
mg: percentuale di mercurio;
al: percentuale di alluminio;
si: percentuale di silicio;
k: percentuale di potassio;
ca: percentuale di calcio;
ba: percentuale di bario;
fe: percentuale di ferro;
Type of Glass:
building_windows_float_processed;
building_windows_non_float_processed;
vehicle_windows_float_processed;
vehicle_windows_non_float_processed (questo tipo di vetro non è presente nel dataset!);
containers;
tableware;
headlamps.
I diversi tipi di vetro possono essere raggruppati in due macro-categorie:
vetro da finestre (edifici o veicoli): classi 1, 2, 3 (la classe 4 non è presente nel dataset);
vetro non da finestre: classi 5, 6, 7;
Costruiamo una nuova variabile window_glass binaria che mappi le calssi come appena definito. Ciò può essere fatto mediante il metodo replace:
glass['window_glass']=glass['Type_of_glass'].replace({1:1,2:1,3:1,5:0,6:0,7:0})
glass.head()
| RI | Na | Mg | Al | Si | K | Ca | Ba | Fe | Type_of_glass | window_glass | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.52101 | 13.64 | 4.49 | 1.10 | 71.78 | 0.06 | 8.75 | 0.0 | 0.0 | 1 | 1 |
| 1 | 1.51761 | 13.89 | 3.60 | 1.36 | 72.73 | 0.48 | 7.83 | 0.0 | 0.0 | 1 | 1 |
| 2 | 1.51618 | 13.53 | 3.55 | 1.54 | 72.99 | 0.39 | 7.78 | 0.0 | 0.0 | 1 | 1 |
| 3 | 1.51766 | 13.21 | 3.69 | 1.29 | 72.61 | 0.57 | 8.22 | 0.0 | 0.0 | 1 | 1 |
| 4 | 1.51742 | 13.27 | 3.62 | 1.24 | 73.08 | 0.55 | 8.07 | 0.0 | 0.0 | 1 | 1 |
22.1. Regressione Logistica Semplice#
Supponiamo adesso di voler indagare la correlazione tra la percentuale di alluminio presente nel vetro (variabile Al) e la variabile dicotomica window_glass. In particolare, vogliamo capire se la variabile Al influenza l’esito di window_glass, ovvero fino a che punto è possibile prevedere il tipo di vetro conoscendo solo la percentuale di alluminio presente. Iniziamo a studiare la correlazione mediante uno scatterplot:
from matplotlib import pyplot as plt
plt.scatter(glass.Al,glass.window_glass)
plt.grid()
plt.show()
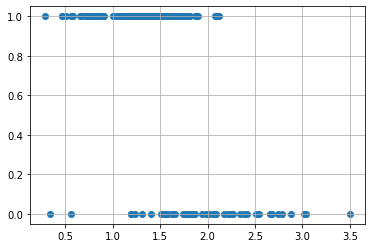
Domanda 1
Sembra esserci una correlazione tra le due variabili? Quale tipo di vetro sembra contere in genere maggiori concentrazioni di alluminio?
22.1.1. Limiti della regressione lineare con variabile dipendente categorica#
Proviamo adesso a visualizzare la retta di regressione relativa alle due variabili:
import seaborn as sns
sns.regplot('Al','window_glass',glass)
plt.grid()
plt.show()
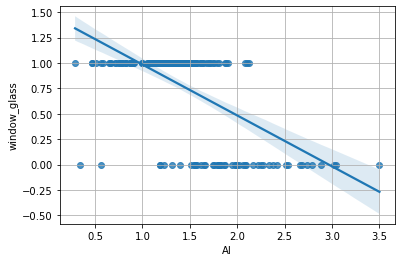
Domanda 2
Guardando il grafico con la retta di regressione, che tipo di vetro prevediamo per i seguenti valori di Al?
Al = 3.5
Al = 0.8
Al = 1.5
Al = 2.5
Al = 0.5
Sulla base di quale criterio basiamo le nostre predizioni?
Il regressore lineare, in pratica, ci permette di ottenere un numero reale che ci da qualche indicazione sul valore più verosimile della variabile dicotomica window_glass. Se il valore ottenuto mediante il regressore lineare è maggiore o uguale a \(0.5\), ha senso prevedere che window_glass sia uguale a 1, altrimenti ha senso prevedere che window_glass sia uguale a 0. Possiamo dunque ottenere delle predizioni binarie sogliando i valori ottenuti mediante il regressore:
from statsmodels.formula.api import ols
#calcoliamo il regressore lineare
model = ols('window_glass ~ Al',glass).fit()
#otteniamo le predizioni
predictions = model.predict(glass)
#arrotondiamo le predizioni al valore più vicino
#ciò corrisponde a sogliare con 0.5
predictions = predictions.round()
#i valori predetti sono adesso binari
predictions.unique()
array([1., 0.])
Plottiamo le predizioni sul grafico di regressione visto prima:
import numpy as np
#ordiniamo i valori di al in ordine crescente
#prima troviamo gli indici che ordinano l'array
idx=np.argsort(glass['Al'])
#poi applichiamo lo stesso ordinamento sia ad al che alle predizioni
al = glass['Al'].values[idx]
pred = predictions.values[idx]
#infine plottiamo
sns.regplot(x='Al',y='window_glass',data=glass)
plt.plot(al,pred,'r')
plt.grid()
plt.show()
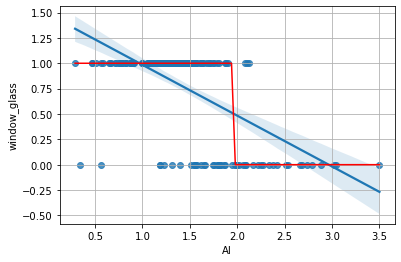
Abbiamo individuato un punto di soglia per al (vicino a \(2.0\)) che permette di distinguere gli elementi appartenenti alle due classi con qualche errore (si pensi ai valori a sinistra di \(2.0\) con classe window_glass pari a zero).
Benché il regressore lineare trovato possa essere utilizzato per la classificazione, esso ha diversi limiti:
Non è chiaro come interpretare i valori ottenuti dal regressore. Si noti che, dato che essi possono essere inferiori a \(0\) o superiori a \(1\), essi non possono essere interpretati come probabilità;
Il metodo non è molto robusto agli outliers. Si immagini che il nostro campione contenga molti punti di classe
window_glasspari a \(0\) e valori dialmolto alti (es. \(300\)). La retta di regressione trovata in questo caso sarebbe molto più orizzontale e molti degli elementi con valori bassi dial(es. \(2.5\)) verrebbero assegnati alla classewindow_glass=0;Il metodo non cattura l’incertezza con la quale possiamo prevedere le classi alle quali appartengono gli elementi. Si considerino ad esempio i punti di valori
al=2.5eal=2.0. Ci aspetteremmo che il modello è “più certo” della classe di appartenenza del primo punto, piuttosto che del secondo.
22.1.2. Regressione Logistica#
Possiamo calcolare un regressore logistico come segue:
from statsmodels.formula.api import logit
model = logit('window_glass ~ Al', glass).fit()
Optimization terminated successfully.
Current function value: 0.354364
Iterations 7
Vedremo come analizzare il regressore e interpretare i coefficienti trovati in seguito.
Possiamo ottenere le probabilità predette per i valori delle variabili indipendenti come segue:
probs = model.predict(glass)
probs.head()
0 0.957513
1 0.883730
2 0.781728
3 0.910590
4 0.926211
dtype: float64
Si noti che i valori ottenuti sono adesso compresi tra \(0\) e \(1\) e dunque interpretabili come probabilità:
probs.min(), probs.max()
(0.0009889852519933211, 0.9985007304335234)
Considereremo un elemento come appartenente alla classe window_glass=1 se la sua probabilità predetta è superiore a \(0.5\). In tal caso infatti, la probabilità di window_glass=0 sarà inferiore a \(0.5\), e dunque l’esito più probabile sarà che l’elemento appartiene alla classe window_glass.
Plottiamo le predizioni come fatto in precedenza:
#riordiniamo le probabilità utilizzando
#gli indici trovati prima
p = probs.values[idx]
sns.regplot(x='Al',y='window_glass',data=glass)
plt.plot(al,p,'r')
plt.grid()
plt.show()
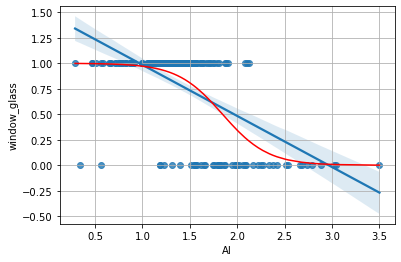
Le probabilità ottenute mostrano adesso “dove” il modello è più incerto e permettono di prevedere la probabilità che un dato elemento sia di classe window_glass=1. Possiamo ottenere un plot di regressione logistica con seaborn come segue:
sns.regplot(glass['Al'],glass['window_glass'],logistic=True)
plt.grid()
plt.show()
/Users/furnari/opt/anaconda3/lib/python3.9/site-packages/seaborn/_decorators.py:36: FutureWarning: Pass the following variables as keyword args: x, y. From version 0.12, the only valid positional argument will be `data`, and passing other arguments without an explicit keyword will result in an error or misinterpretation.
warnings.warn(
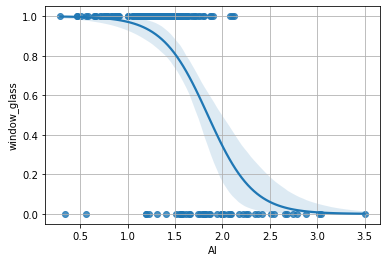
Domanda 3
Il regressore logistico individua, in maniera simile a quanto visto per il regressore lineare, una soglia oltre la quale i punti vengono assegnati a una classe piuttosto che a un’altra. Si confronti questo punto di soglia con quello ottenuto nel caso del regressore lineare. I due punti sono diversi? Perché?
22.1.3. Analisi del regressore logistico#
Visualizziamo il summary del regressore logistico calcolato in precedenza:
model.summary()
| Dep. Variable: | window_glass | No. Observations: | 214 |
|---|---|---|---|
| Model: | Logit | Df Residuals: | 212 |
| Method: | MLE | Df Model: | 1 |
| Date: | Tue, 31 Oct 2023 | Pseudo R-squ.: | 0.3547 |
| Time: | 07:41:22 | Log-Likelihood: | -75.834 |
| converged: | True | LL-Null: | -117.51 |
| Covariance Type: | nonrobust | LLR p-value: | 6.835e-20 |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 7.7136 | 1.078 | 7.158 | 0.000 | 5.602 | 9.826 |
| Al | -4.1804 | 0.660 | -6.338 | 0.000 | -5.473 | -2.888 |
22.1.3.1. Significatività#
Il summary presenta diversi elementi. Analizziamone i più importanti:
Pseudo R-squared: va interpretato come l’R-Squared nel caso della regressione lineare. Ci dice quanto il modello “spiega” bene i dati;
LLR p-value: è il p-value calcolato da un “Likelihood-ratio test” (Rapporto di verosimiglianza). Se il valore del p-value è al di sotto di una soglia critica, (es. \(0.0\)), il regressore logistico è statisticamente rilevante;
P-value dei coefficienti (\(P>|z|\)): vanno interpretati come nel caso della regressione lineare. P-value piccoli indicano che le variabili coinvolte contribuiscono significativamente alla regressione.
Nel caso specifico del regressore allenato, possiamo dire che:
Il regressore logistico spiega parte della relazione tra le variabili (pseudo \(R^2\) pari a circa \(0.35\));
Il regressore logistico è statisticamente rilevante (p-value al di sotto di \(0.05\));
I coefficienti sono tutti statisticamente rilevanti (p-value bassi);
22.1.3.2. Analisi dei coefficienti#
Analizziamo i coefficienti del regressore logistico calcolato prima. Visualizziamo nuovamente il summary:
model.summary()
| Dep. Variable: | window_glass | No. Observations: | 214 |
|---|---|---|---|
| Model: | Logit | Df Residuals: | 212 |
| Method: | MLE | Df Model: | 1 |
| Date: | Tue, 31 Oct 2023 | Pseudo R-squ.: | 0.3547 |
| Time: | 07:41:53 | Log-Likelihood: | -75.834 |
| converged: | True | LL-Null: | -117.51 |
| Covariance Type: | nonrobust | LLR p-value: | 6.835e-20 |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 7.7136 | 1.078 | 7.158 | 0.000 | 5.602 | 9.826 |
| Al | -4.1804 | 0.660 | -6.338 | 0.000 | -5.473 | -2.888 |
Calcoliamo l’esponenziale dei valori dei coefficienti:
np.exp(model.params)
Intercept 2238.577657
Al 0.015292
dtype: float64
Possiamo dire che:
Per \(al=0\), l’odds che il vetro sia da finestra (
window_glass=1) è pari a circa \(2238\). E’ dunque \(2238\) volte più probabile che il vetro sia da finestra;L’incremento di una unità del valore della variabile
alcorrisponde a un incremento moltiplicativo di \(0.015\). Dato che il numero è minore di 1, ciò corrisponde a un decremento moltiplicativo pari a \(1-0.015=0.985\). Possiamo dire dunque che l’incremento di una unità del valore dialcorrisponde a un decremento del \(98.5\%\) dell’odds.
Domanda 4
Le considerazioni tratte dall’analisi dei coefficienti sono coerenti con quanto visualizzato nel plot di regressione logistica visto in precedenza?
22.2. Regressione Logistica Multipla#
E’ possibile calcolare un regressore logistico a partire da più variabili indipendenti semplicemente rivedendo il modello come:
\begin{equation} logit(p)=\beta_0 + \beta_1 x_1 + \ldots + \beta_n x_n \end{equation}
Proviamo a calcolare il modello scegliendo come variabili indipendenti na e si e mantenendo window_glass come variabile dipendente. Possiamo visualizzare lo scatterplot con le classi evidenziate utilizzando searborn:
plt.figure(figsize=(12,8))
sns.scatterplot(x='Na',y='Si',data=glass, hue='window_glass')
plt.show()
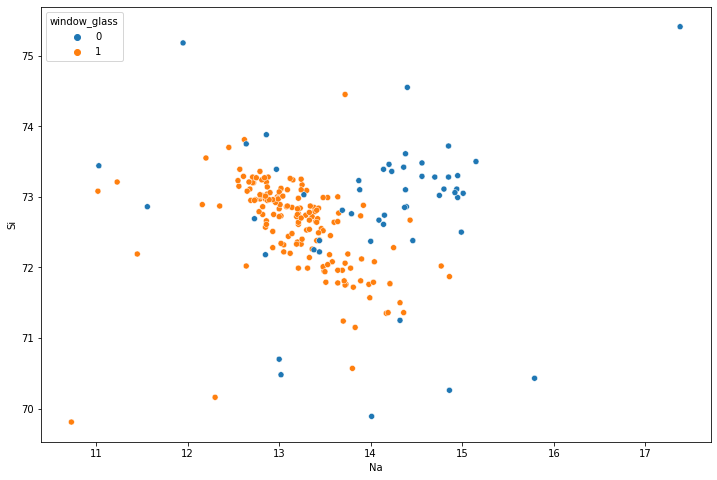
Domanda 5
Come si distribuiscono i dati delle due classi nello spazio? Quale potrebbe essere un buon criterio per classificarli?
Calcoliamo il regressore logistico multiplo:
model = logit('window_glass ~ Na + Si',glass).fit()
model.summary()
Optimization terminated successfully.
Current function value: 0.409695
Iterations 7
| Dep. Variable: | window_glass | No. Observations: | 214 |
|---|---|---|---|
| Model: | Logit | Df Residuals: | 211 |
| Method: | MLE | Df Model: | 2 |
| Date: | Tue, 31 Oct 2023 | Pseudo R-squ.: | 0.2539 |
| Time: | 07:43:20 | Log-Likelihood: | -87.675 |
| converged: | True | LL-Null: | -117.51 |
| Covariance Type: | nonrobust | LLR p-value: | 1.098e-13 |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 91.9716 | 22.944 | 4.008 | 0.000 | 47.002 | 136.941 |
| Na | -1.8780 | 0.306 | -6.143 | 0.000 | -2.477 | -1.279 |
| Si | -0.8988 | 0.292 | -3.075 | 0.002 | -1.472 | -0.326 |
Analizziamo in breve il risultato della regressione logistica:
Il modello spiega parte della relazione tra le variabili indipendenti e la variabile dipendente (\(R^2=0.2539\));
Il regressore si distingue in maniera rilevante dal regressore nullo (p-value sotto la soglia critica \(0.05\));
I parametri del regressore sono tutti statisticamente rilevanti (p-value tutti sotto la soglia \(0.05\)); Calcoliamo l’esponenziale dei parametri:
np.exp(model.params)
Intercept 8.764972e+39
Na 1.528937e-01
Si 4.070460e-01
dtype: float64
Se
Na=0eSi=0, il vetro è da finestra in maniera quasi certa;Se la variabile
Si=0, l’incremento di una unità della variabilenacausa un decremento dell’odds di circa il \(98.48\%\);Se la variabile
Na=0, l’incremento di una unità della variabilesicausa un decremento dell’odds pari a circa il \(96\%\).
Domanda 6
Considerato che
SieNahanno la stessa unità di misura (misurano entrambe delle concentrazioni), quali delle due variabili influenza maggiormente l’esito dell’appartenenza o meno alla classewindow_glass? Se le unità di misura fossero diverse, potremmo fare le stesse considerazioni?
22.2.1. Esempio di regressione logistica con più di due variabili indipendenti#
Vediamo un esempio di regressione logistica con più di due variabili indipendenti. Utilizzeremo il dataset di R biopsy. Possiamo caricarlo mediante statsmodels:
from statsmodels.datasets import get_rdataset
biopsy = get_rdataset('biopsy',package='MASS')
print(biopsy.__doc__)
.. container::
====== ===============
biopsy R Documentation
====== ===============
.. rubric:: Biopsy Data on Breast Cancer Patients
:name: biopsy
.. rubric:: Description
:name: description
This breast cancer database was obtained from the University of
Wisconsin Hospitals, Madison from Dr. William H. Wolberg. He assessed
biopsies of breast tumours for 699 patients up to 15 July 1992; each
of nine attributes has been scored on a scale of 1 to 10, and the
outcome is also known. There are 699 rows and 11 columns.
.. rubric:: Usage
:name: usage
.. code:: R
biopsy
.. rubric:: Format
:name: format
This data frame contains the following columns:
``ID``
sample code number (not unique).
``V1``
clump thickness.
``V2``
uniformity of cell size.
``V3``
uniformity of cell shape.
``V4``
marginal adhesion.
``V5``
single epithelial cell size.
``V6``
bare nuclei (16 values are missing).
``V7``
bland chromatin.
``V8``
normal nucleoli.
``V9``
mitoses.
``class``
``"benign"`` or ``"malignant"``.
.. rubric:: Source
:name: source
P. M. Murphy and D. W. Aha (1992). UCI Repository of machine learning
databases. [Machine-readable data repository]. Irvine, CA: University
of California, Department of Information and Computer Science.
O. L. Mangasarian and W. H. Wolberg (1990) Cancer diagnosis via
linear programming. *SIAM News* **23**, pp 1 & 18.
William H. Wolberg and O.L. Mangasarian (1990) Multisurface method of
pattern separation for medical diagnosis applied to breast cytology.
*Proceedings of the National Academy of Sciences, U.S.A.* **87**, pp.
9193–9196.
O. L. Mangasarian, R. Setiono and W.H. Wolberg (1990) Pattern
recognition via linear programming: Theory and application to medical
diagnosis. In *Large-scale Numerical Optimization* eds Thomas F.
Coleman and Yuying Li, SIAM Publications, Philadelphia, pp 22–30.
K. P. Bennett and O. L. Mangasarian (1992) Robust linear programming
discrimination of two linearly inseparable sets. *Optimization
Methods and Software* **1**, pp. 23–34 (Gordon & Breach Science
Publishers).
.. rubric:: References
:name: references
Venables, W. N. and Ripley, B. D. (2002) *Modern Applied Statistics
with S-PLUS.* Fourth Edition. Springer.
Il dataset contiene \(699\) osservazioni e \(11\) colonne. Ogni osservazioni contiene misurazioni di \(9\) grandezze relative a campioni di tessuto che possono essere tumori “benigni” o “maligni”. Iniziamo manipolando un po’ i dati. Visualizziamo i valori della variabile class:
biopsy.data['class'].unique()
array(['benign', 'malignant'], dtype=object)
Per calcolare il modello di regressione logistica mediante statsmodels è necessario convertire questi valori in interi (\(0\) o \(1\)). Inoltre, conviene evitare di chiamare la colonna class in quanto questa è una parola riservata per statsmodels. Costruiamo una nuova colonna cl che contiene i valori di class modificati:
biopsy.data['cl'] = biopsy.data['class'].replace({'benign':0, 'malignant':1})
Procediamo a calcolare il regressore logistico considerando tutte le variabili:
model = logit('cl ~ V1 + V2 + V3 + V4 + V5 + V6 + V7 + V8 + V9',biopsy.data).fit()
model.summary()
Optimization terminated successfully.
Current function value: 0.075321
Iterations 10
| Dep. Variable: | cl | No. Observations: | 683 |
|---|---|---|---|
| Model: | Logit | Df Residuals: | 673 |
| Method: | MLE | Df Model: | 9 |
| Date: | Tue, 31 Oct 2023 | Pseudo R-squ.: | 0.8837 |
| Time: | 07:44:51 | Log-Likelihood: | -51.444 |
| converged: | True | LL-Null: | -442.18 |
| Covariance Type: | nonrobust | LLR p-value: | 2.077e-162 |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | -10.1039 | 1.175 | -8.600 | 0.000 | -12.407 | -7.801 |
| V1 | 0.5350 | 0.142 | 3.767 | 0.000 | 0.257 | 0.813 |
| V2 | -0.0063 | 0.209 | -0.030 | 0.976 | -0.416 | 0.404 |
| V3 | 0.3227 | 0.231 | 1.399 | 0.162 | -0.129 | 0.775 |
| V4 | 0.3306 | 0.123 | 2.678 | 0.007 | 0.089 | 0.573 |
| V5 | 0.0966 | 0.157 | 0.617 | 0.537 | -0.210 | 0.404 |
| V6 | 0.3830 | 0.094 | 4.082 | 0.000 | 0.199 | 0.567 |
| V7 | 0.4472 | 0.171 | 2.609 | 0.009 | 0.111 | 0.783 |
| V8 | 0.2130 | 0.113 | 1.887 | 0.059 | -0.008 | 0.434 |
| V9 | 0.5348 | 0.329 | 1.627 | 0.104 | -0.110 | 1.179 |
Il regressore logistico spiega bene la relazione tra le variabili (\(R^2\) alto) ed è significativo (p-value quasi nullo). Alcuni coefficienti hanno un p-value alto. Iniziamo eliminando la variabile V2, che ha il p-value più alto:
model = logit('cl ~ V1 + V3 + V4 + V5 + V6 + V7 + V8 + V9',biopsy.data).fit()
model.summary()
Optimization terminated successfully.
Current function value: 0.075321
Iterations 10
| Dep. Variable: | cl | No. Observations: | 683 |
|---|---|---|---|
| Model: | Logit | Df Residuals: | 674 |
| Method: | MLE | Df Model: | 8 |
| Date: | Tue, 31 Oct 2023 | Pseudo R-squ.: | 0.8837 |
| Time: | 07:45:00 | Log-Likelihood: | -51.445 |
| converged: | True | LL-Null: | -442.18 |
| Covariance Type: | nonrobust | LLR p-value: | 2.036e-163 |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | -10.0976 | 1.155 | -8.739 | 0.000 | -12.362 | -7.833 |
| V1 | 0.5346 | 0.141 | 3.784 | 0.000 | 0.258 | 0.811 |
| V3 | 0.3182 | 0.174 | 1.826 | 0.068 | -0.023 | 0.660 |
| V4 | 0.3299 | 0.121 | 2.723 | 0.006 | 0.092 | 0.567 |
| V5 | 0.0961 | 0.156 | 0.618 | 0.537 | -0.209 | 0.401 |
| V6 | 0.3831 | 0.094 | 4.082 | 0.000 | 0.199 | 0.567 |
| V7 | 0.4465 | 0.170 | 2.628 | 0.009 | 0.114 | 0.779 |
| V8 | 0.2125 | 0.112 | 1.902 | 0.057 | -0.006 | 0.432 |
| V9 | 0.5341 | 0.328 | 1.630 | 0.103 | -0.108 | 1.176 |
Procediamo rimuovendo V5, che ha p-value pari a \(0.537\):
model = logit('cl ~ V1 + V3 + V4 + V6 + V7 + V8 + V9',biopsy.data).fit()
model.summary()
Optimization terminated successfully.
Current function value: 0.075598
Iterations 10
| Dep. Variable: | cl | No. Observations: | 683 |
|---|---|---|---|
| Model: | Logit | Df Residuals: | 675 |
| Method: | MLE | Df Model: | 7 |
| Date: | Tue, 31 Oct 2023 | Pseudo R-squ.: | 0.8832 |
| Time: | 07:45:02 | Log-Likelihood: | -51.633 |
| converged: | True | LL-Null: | -442.18 |
| Covariance Type: | nonrobust | LLR p-value: | 2.240e-164 |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | -9.9828 | 1.126 | -8.865 | 0.000 | -12.190 | -7.776 |
| V1 | 0.5340 | 0.141 | 3.793 | 0.000 | 0.258 | 0.810 |
| V3 | 0.3453 | 0.172 | 2.012 | 0.044 | 0.009 | 0.682 |
| V4 | 0.3425 | 0.119 | 2.873 | 0.004 | 0.109 | 0.576 |
| V6 | 0.3883 | 0.094 | 4.150 | 0.000 | 0.205 | 0.572 |
| V7 | 0.4619 | 0.168 | 2.746 | 0.006 | 0.132 | 0.792 |
| V8 | 0.2261 | 0.111 | 2.037 | 0.042 | 0.009 | 0.444 |
| V9 | 0.5312 | 0.324 | 1.637 | 0.102 | -0.105 | 1.167 |
Rimuoviamo V9, che ha p-value superiore a \(0.05\):
model = logit('cl ~ V1 + V3 + V4 + V6 + V7 + V8',biopsy.data).fit()
model.summary()
Optimization terminated successfully.
Current function value: 0.078436
Iterations 9
| Dep. Variable: | cl | No. Observations: | 683 |
|---|---|---|---|
| Model: | Logit | Df Residuals: | 676 |
| Method: | MLE | Df Model: | 6 |
| Date: | Tue, 31 Oct 2023 | Pseudo R-squ.: | 0.8788 |
| Time: | 07:45:06 | Log-Likelihood: | -53.572 |
| converged: | True | LL-Null: | -442.18 |
| Covariance Type: | nonrobust | LLR p-value: | 1.294e-164 |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | -9.7671 | 1.085 | -9.001 | 0.000 | -11.894 | -7.640 |
| V1 | 0.6225 | 0.137 | 4.540 | 0.000 | 0.354 | 0.891 |
| V3 | 0.3495 | 0.165 | 2.118 | 0.034 | 0.026 | 0.673 |
| V4 | 0.3375 | 0.116 | 2.920 | 0.004 | 0.111 | 0.564 |
| V6 | 0.3786 | 0.094 | 4.035 | 0.000 | 0.195 | 0.562 |
| V7 | 0.4713 | 0.166 | 2.837 | 0.005 | 0.146 | 0.797 |
| V8 | 0.2432 | 0.109 | 2.240 | 0.025 | 0.030 | 0.456 |
Tutti i coefficienti hanno adesso un p-value accettabile. Proseguiamo all’analisi dei coefficienti. Calcoliamo gli esponenziali:
np.exp(model.params)
Intercept 0.000057
V1 1.863641
V3 1.418374
V4 1.401487
V6 1.460166
V7 1.602133
V8 1.275287
dtype: float64
Il valore dell’esponenziale dell’intercetta quasi nullo indica che, quando tutte le variabili assumono valori nulli, l’odds è molto basso. Ciò indica che \(p\) è basso, mentre \(1-p\) è molto alto. La probabilità di avere un tumore maligno è quindi molto bassa se tutte le variabili assumono valori nulli;
L’incremento di una unità del valore di
V1corrisponde all’incremento di circa l’\(86\%\) dell’odds, il che rende la possibilità di un tumore maligno più alta;L’incremento di una unità del valore di
V3corrisponde all’incremento di circa il \(41\%\) dell’odds;L’incremento di una unità del valore di
V4corrisponde all’incremento di circa il \(40\%\) dell’odds;L’incremento di una unità del valore di
V6corrisponde all’incremento di circa il \(46\%\) dell’odds;L’incremento di una unità del valore di
V7corrisponde all’incremento di circa il \(60\%\) dell’odds;L’incremento di una unità del valore di
V8corrisponde all’incremento di circa il \(27\%\) dell’odds;
L’incremento delle variabili, in genere, causa un incremento dell’odds. Pertanto ci aspettiamo che i valori delle variabili siano piccoli in presenza di tumori benigni.
Domanda 7
Si legga la documentazione del dataset considerato per capire su quale scala sono stati registrati i valori delle variabili indipendenti. Si calcolino inoltre le deviazioni standard delle singole variabili nel dataset. Possiamo dire che qualcuna di queste variabili è più influente sulla presenza di un tumore maligno rispetto alle altre?
22.3. Regressore Logistico Multinomiale (Opzionale)#
Vediamo un esempio di regressore logistico multinomiale sul dataset delle Iris di Fisher. Carichiamo il dataset con seaborn:
import seaborn as sns
iris = sns.load_dataset('iris')
iris
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
| ... | ... | ... | ... | ... | ... |
| 145 | 6.7 | 3.0 | 5.2 | 2.3 | virginica |
| 146 | 6.3 | 2.5 | 5.0 | 1.9 | virginica |
| 147 | 6.5 | 3.0 | 5.2 | 2.0 | virginica |
| 148 | 6.2 | 3.4 | 5.4 | 2.3 | virginica |
| 149 | 5.9 | 3.0 | 5.1 | 1.8 | virginica |
150 rows × 5 columns
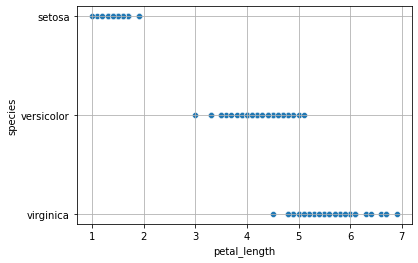
Come visto a lezione, considereremo intanto una unica feature petal_length:
sns.scatterplot(x='petal_length', y='species', data=iris)
plt.grid()
plt.show()
Posso calcolare il regressore multinomiale mediante MNLogit di statsmodels. Prima però dovrò effettuare un mapping delle classe su valori interi:
from statsmodels.formula.api import mnlogit
iris2 = iris.copy();
iris2['species'] = iris2['species'].replace({'setosa':2, 'versicolor':1, 'virginica':0})
mnlogit("species ~ sepal_length", iris2).fit().summary()
Optimization terminated successfully.
Current function value: 0.606893
Iterations 8
| Dep. Variable: | species | No. Observations: | 150 |
|---|---|---|---|
| Model: | MNLogit | Df Residuals: | 146 |
| Method: | MLE | Df Model: | 2 |
| Date: | Tue, 31 Oct 2023 | Pseudo R-squ.: | 0.4476 |
| Time: | 07:49:17 | Log-Likelihood: | -91.034 |
| converged: | True | LL-Null: | -164.79 |
| Covariance Type: | nonrobust | LLR p-value: | 9.276e-33 |
| species=1 | coef | std err | z | P>|z| | [0.025 | 0.975] |
|---|---|---|---|---|---|---|
| Intercept | 12.6771 | 2.906 | 4.362 | 0.000 | 6.981 | 18.373 |
| sepal_length | -2.0307 | 0.466 | -4.361 | 0.000 | -2.943 | -1.118 |
| species=2 | coef | std err | z | P>|z| | [0.025 | 0.975] |
| Intercept | 38.7590 | 5.691 | 6.811 | 0.000 | 27.605 | 49.913 |
| sepal_length | -6.8464 | 1.022 | -6.698 | 0.000 | -8.850 | -4.843 |
Il regressore logistico multinomiale è statisticamente rilevante (p-value basso) e che tutti i coefficienti hanno p-value bassi.
Possiamo notare che ci sono due insiemi di coefficienti: uno per species=1 (versicolor) e uno per species=2 (setosa). Non sono stati stimati coefficienti per virginica, perché è stata scelta come linea di base. Tutti i valori p sono bassi, quindi possiamo mantenere tutte le variabili. Vediamo come interpretare i coefficienti:
L’intercetta per
species=1è \(12.6771\). Ciò indica che la probabilità diversicolorrispetto avirginicaè \(e^{12.6771}=320327.76\), quandosepal_lengthè impostato a zero. Questo è un numero molto grande, probabilmente a causa del fatto chesepal_length=0non è un’osservazione realistica.L’intercetta per
species=2è \(38.7590\). Ciò indica che la probabilità disetosarispetto avirginicaè \(e^{38.7590}=6.8e+16\), quandosepal_lengthè impostato a zero. Anche in questo caso, otteniamo un numero molto grande, probabilmente a causa del fatto chesepal_length=0non è un’osservazione realistica.Il coefficiente \(-2.0307\) di
sepal_lengthperspecies=1indica che quando osserviamo un aumento di un centimetro disepal_length, la probabilità diversicolorrispetto avirginicadiminuisce moltiplicativamente del \(e^{-2.0307} = 0.13\) (una diminuzione del -87%).Il coefficiente \(-6.8564\) di
sepal_lengthperspecies=2indica che quando osserviamo un aumento di un centimetro disepal_length, la probabilità disetosarispetto avirginicadiminuisce moltiplicativamente del \(e^{-6.8464} = 0.001\) (una diminuzione del -99.9%).
22.4. Esercizi#
Esercizio 1
Si calcoli un regressore logistico per predire i valori della variabile
Surviveda partire dalle altre variabili del dataset Titanic. Si gestiscano adeguatamente le variabili categoriche. Si utilizzi il metodo della backward elimination per eliminare le variabili che non contribuiscono significativamente alla regressione. Si analizzi il regressore trovato e si discuta il significato dei suoi parametri.
Esercizio 2
Si scelgano due variabili significative del regressore calcolato al punto precedente e si calcoli un regressore bivariato usando solo queste due variabili. Si visualizzi un plot di regressione logistica sui dati bidimensionali individuati dalle due variabili. Si plotti il decision boundary individuato dal regressore sullo scatterplot delle due variabili.
Esercizio 3
Si consideri il dataset Boston. Si costruisca un regressore logistico per prevedere i valori della variabile
chasa partire dai valori delle altre variabili. Si gesticano adeguatamente le variabili categoriche mediante l’introduzione di variabili dummy. Si utilizzi il metodo della backward elimination per eliminare le variabili che non contribuiscono significativamente alla regressione.

