4. Misure di Tendenza Centrale, Dispersione e Forma#
La statistica descrittiva si occupa di descrivere, rappresentare e sintetizzare un campione di dati relativo ad una popolazione. Gli strumenti della statistica descrittiva possono essere sia numerici che grafici. I dati analizzati possono essere descritti secondo diversi aspetti. Esistono pertanto diversi “indicatori” oggettivi:
numerosità del campione;
indicatori centrali: media, mediana, moda;
Indicatori di dispersione: estremi, range, quantili, percentili, quartili, distanza inter-quartile, varianza;
Per esaminare questi strumenti, iniziamo considerando un semplice campione univariato:
0 3.0
1 4.0
2 NaN
3 4.0
4 4.0
5 1.0
6 2.0
7 2.0
8 NaN
9 4.0
dtype: float64
Il campione contiene dei valori NaN. Si tratta di valori mancanti che per qualche motivo non sono stati rilevati e andranno gestiti opportunamente.
4.1. Numerosità#
La numerosità di un campione univariato \(\{x^{(i)}\}_i^N\) è data dal numero di valori in esso contenuto: \(|\{x^{(i)}\}_i^N| = N\). La numerosità di ciascuna colonna può anche essere diversa in quanto possono essistere dei valori mancanti, indicati in genere con NA o NaN. Nel nostro caso:
<class 'pandas.core.series.Series'>
RangeIndex: 10 entries, 0 to 9
Series name: None
Non-Null Count Dtype
-------------- -----
8 non-null float64
dtypes: float64(1)
memory usage: 208.0 bytes
Il sommario sopra indica che, sebbene abbiamo \(10\) valori, solo \(8\) di questi sono non nulli.
4.2. Indicatori di tendenza centrale#
Gli indicatori centrali danno un’idea approssimata dell’ordine di grandezza dei valori del campione.
4.2.1. Media#
La media di un campione è definita come la somma dei suoi valori diviso la sua numerosità:
La media del nostro campione sarà:
3.0
4.2.2. Mediana#
Quando gli elementi di un campione possono essere ordinati (ad esempio se sono valori numerici), la mediana di un campione (o l’elemento mediano) è l’elemento che divide in due parti uguali l’insieme ordinato dei valori del campione.
L’elemento mediano si può ottenere ordinando i valori del campione e procedendo come segue:
Se il numero di elementi è dispari, si prende l’elemento centrale. Ad esempio \([1,2,\mathbf{2},3,5] \to 2\).
Se il numero di elementi è pari, si prende la media tra i due centrali. Ad esempio \([1,2,\mathbf{2},\mathbf{3},3,5] \to \frac{2+3}{2} = 2.5\).
Nel caso del nostro campione:
5 1.0
6 2.0
7 2.0
0 3.0
1 4.0
3 4.0
4 4.0
9 4.0
2 NaN
8 NaN
dtype: float64
Valore mediano: 3.5
Da un punto di vista formale, se abbiamo \(n\) osservazioni \(x^{(1)}, \ldots, x^{(1)}\), che possono essere ordinate come \(x^{(i_i)},\ldots, x^{(i_n)}\), il calcolo della mediana può essere espresso come segue:
4.2.3. Quantili, Percentili e Quartili#
Quantili, percentili e quartili generalizzano il concetto di mediana.
4.2.3.1. Quantili#
Un quantile di ordine \(\alpha\) è un valore \(q_\alpha\) che divide un campione in due parti di dimensioni proprozionali a \(\alpha\) e \(1-\alpha\). Valori più piccoli o uguali a \(q_\alpha\) appartengono alla prima parte della suddivisione, mentre valori maggiori a \(q_\alpha\) appartengono alla seconda parte.
Ad esempio, dato il campione già ordinato [1,2,3,3,4,5,6,6,7,8,8,9], un quantile \(q_{0.25}\) dividerà il campione in due parti di dimensione proporzionale a \(0.25\) e \(1-0.25=0.75\). In questo caso \(q_{0.25}=3\) e le due parti saranno [1,2,3,3] e [4,5,6,6,7,8,8,9].
Anche in questo caso, come nel caso della mediana, si effettuano medie di valori adiacenti ove opportuno.
I quantili vanno interpretati così:
Se un quantile di ordine \(\alpha\) è pari al numero \(x\), allora vuole dire che \(\alpha \times n\) elementi hanno un valore inferiore o uguale a \(x\), dove \(n\) è il numero di elementi nel campione.
Va notato che:
Il minimo è un quantile di ordine 0;
Il massimo è un quantile di ordine 1;
La mediana è un quantile di ordine 0.5.
Vediamo alcuni esempi sul nostro piccolo campione:
Quantile di ordine 0 (minimo): 1.0
Quantile di ordine 0.5 (mediana): 3.5
Quantile di ordine 1 (massimo): 4.0
Quantile di ordine 0.15: 2.0
Dai dati sopra deduciamo che:
Il \(50\%\) dei valori sono inferiori o uguali a 3;
Il \(15\%\) dei valori sono minori o ugualei a 2.
4.2.3.2. Percentili#
I percentili sono semplicemente quantili espressi in precentuale. Un quantile di ordine \(0.25\) è un percentile di ordine \(25\%\).
4.2.3.3. Quartili#
I quartili sono degli specifici quantili che suddividono il campione in quattro parti. In particolare:
Il quartile di ordine 0 è un quantile di ordine 0;
Il quartile di ordine 1 è un quantile di ordine \(1/4=0.25\);
Il quartile di ordine 2 è un quantile di ordine \(2/4=0.5\);
Il quartile di ordine 3 è un quantile di ordine \(3/4=0.75\);
Il quartile di ordine 4 è un qauntile di ordine \(4/4=1\).
Vediamo qualche esempio sul nostro piccolo campione:
Quartile di ordine 0 (minimo): 1.0
Quartile di ordine 1: 2.0
Quartile di ordine 2 (mediana): 3.5
Quartile di ordine 3: 4.0
Quartile di ordine 4 (massimo): 4.0
4.2.4. Moda#
La moda di un campione è l’elemento che si ripete più spesso. Ad esempio, consideriamo il seguente campione:
0 1
1 2
2 3
3 4
4 2
5 5
6 4
7 2
8 6
9 5
10 8
11 4
12 3
13 2
14 3
dtype: int64
Consideriamo dunque le frequenze assolute:
2 4
3 3
4 3
5 2
1 1
6 1
8 1
dtype: int64
La moda sarà pari a \(4\).
In termini formali, la moda \(\overline x_M\) del campione visto prima sarà data da:
Dove \(a_j\) sono i valori univoci del campione e \(n_j\) sono le relative frequenze.
4.3. Indicatori di dispersione#
Gli indici di dispersione hanno il compito di quantificare in quale misura i valori di una distribuzione sono “dispersi”, ovvero “lontani tra loro”.
4.3.1. Minimo, Massimo e Range#
Semplici indici di dispersione sono il minimo (\(min \{x^{(i)}\}_i^N\)), il massimo (\(max \{x^{(i)}\}_i^N\)) e il range (\(max \{x^{(i)}\}_i^N\) - \(min \{x^{(i)}\}_i^N\)). Tornando al ultimo esempio:
0 1
1 2
2 3
3 4
4 2
5 5
6 4
7 2
8 6
9 5
10 8
11 4
12 3
13 2
14 3
dtype: int64
Avremo che:
Minimo: 1
Massimo: 8
Range: 7
4.3.2. Distanza interquartile#
Il range non è un indice di dispersione molto robusto, in quanto non tiene conto della presenza di evenutali outliers. Si considerino ad esempio i seguenti campioni “artificiali”:
s1 s2
0 3.000000 -5.000000
1 3.444444 3.444444
2 3.888889 3.888889
3 4.333333 4.333333
4 4.777778 4.777778
5 5.222222 5.222222
6 5.666667 5.666667
7 6.111111 6.111111
8 6.555556 6.555556
9 7.000000 15.000000
Range sample 1: 4.0
Range sample 2: 20.0
I campioni sono simili, ma la presenza di due outliers (-5 e 15) nel secondo campione rende i range molto diversi (4 e 20).
Confrontando i due boxplot mostrati sopra, notiamo che le posizioni del terzo e del primo quartile sono più “robuste” agli outliers. Una misura di dispersione un po’ più espressiva è dunque lo scarto interquartile (o distanza interquartile), che si misura come la differenza tra il terzo e il primo quartile:
Lo scarto interquartile di sample 1 è: 2.0
Lo scarto interquartile di sample 2 è: 2.0
4.3.3. Varianza e Deviazione Standard#
La varianza (detto anche scarto quadratico medio) fornisce una stima di quanto i dati osservati si allontanano dalla media. La varianza calcola la media dei quadrati degli scarti dei valori rispetto alla media, penalizzando i grandi scostamenti dal valore medio (dovuti agli outliers) maggiormente rispetto ai piccoli scostamenti:
Possiamo attribuire un significato geometrico alla varianza, come mostrato nel grafico sotto:
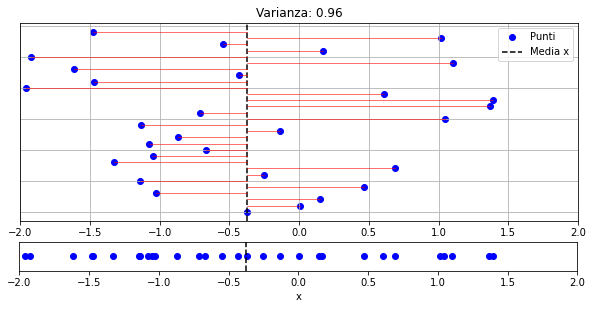
Nel grafico, il plot in basso mostra un campione univariato \(\{x_i\}_i^N\). Il plot in alto, mostra lo stesso campione “esploso” sull’asse \(y\) per questioni di visualizzazione. Nel plot in alto, la linea nera tratteggiata indica la media di del campione, mentre le linee rosse sono i termini \((x_i-\overline x)\) che appaiono nella formula della varianza. La varianza calcola la media delle lunghezze di questi segmenti.
Il grafico che segue mostra un campione meno “disperso”:
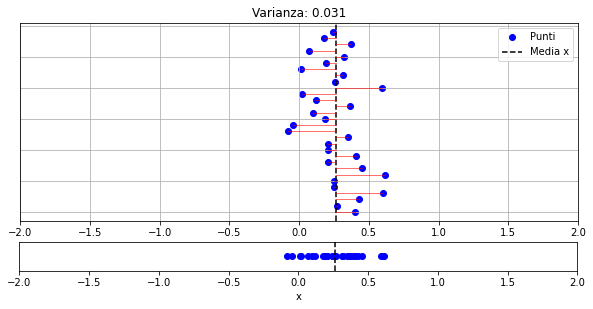
La varianza del nostro piccolo campione sarà:
3.3999999999999995
Gli indici di dispersione visti fino ad ora (esclusa la varianza) hanno come unità di misura la stessa dei dati di input. Nel caso dei pesi, i dati vengono misurati in libbre. E’ pertanto corretto dire che minimo, massimo, range, scarto interquartile e scarto medio assoluto calcolati sui pesi si misurano in libbre.
Lo stesso discorso non vale per la varianza, che si misurera in libbre al quadrato. Se vogliamo ottenere una misura di dispersione commensurabile, possiamo calcolare la radice quadrata della varianza, ottenendo così la deviazione standard (o scarto quadratico medio), che si definisce come segue:
Consideriamo nuovamente il nostro dataset di pesi e altezze. Le medie e deviazioni standard delle due variabili pesi e altezze sono:
| height | weight | |
|---|---|---|
| mean | 66.826046 | 35.818062 |
| std | 4.002658 | 7.987908 |
La deviazione standard ci dice qualcosa anche sulla “forma” della distribuzione. Confrontiamo ad esempio le deviazioni standard delle altezze di uomini e donne:
sex
F 2.686187
M 2.911766
Name: height, dtype: float64
Dal confronto notiamo che le altezze degli uomini sono “più disperse” (hanno cioè una deviazione standard più alta). Confrontiamo le stime di densità dei due campioni:
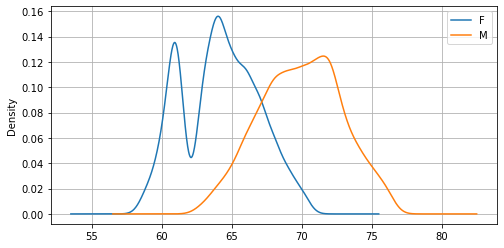
Notiamo che in effetti la stima di densità per gli uomini ha individuato una curva più “spanciata”, che si correla bene con la più alta devizione standard.
4.3.4. Normalizzazioni dei Dati#
Gli indicatori di dispersione dei dati visti dipendono fortemente dalla natura dei dati e dalla loro unità di misura. Ad esempio, le età si misurano in anni, mentre i pesi in Kg o libbre. Pertanto, esistono delle tecniche di normalizzazione dei dati che permettono di rendere dati basati su unità di misura diverse comparabili tra di loro.
4.3.4.1. Normalizzazione tra 0 e 1#
Questa normalizzazione scala i dati in modo che i valori minimo e massimo risultino esattamente pari a \(0\) e \(1\), usando la seguente formula:
Nel caso del nostro campione, otterremmo:
0 0.000000
1 0.142857
2 0.285714
3 0.428571
4 0.142857
5 0.571429
6 0.428571
7 0.142857
8 0.714286
9 0.571429
10 1.000000
11 0.428571
12 0.285714
13 0.142857
14 0.285714
dtype: float64
4.3.4.2. Normalizzazione tra -1 e 1#
In questo caso, i dati vengono riscalati in modo che i nuovi minimo e massimo siano \(-1\) e \(1\), usando la seguente formula:
Possiamo effettuare questa trasformazione in Pandas come segue:
0 1.000000
1 0.714286
2 0.428571
3 0.142857
4 0.714286
5 -0.142857
6 0.142857
7 0.714286
8 -0.428571
9 -0.142857
10 -1.000000
11 0.142857
12 0.428571
13 0.714286
14 0.428571
dtype: float64
4.3.4.3. Standardizzazione (z-scoring)#
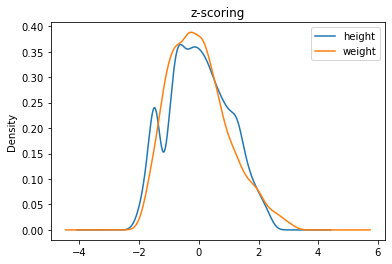
In molti casi è utile normalizzare i dati in modo che essi presentino media nulla e deviazione standard unitaria. Questo tipo di normalizzazione viene detta “z-scoring” e viene effettuata sottraendo ai dati la media e dividendo per la deviazione standard.
dove \(s_x\) è la deviazione standard della popolazione alla quale appartiene \(X\). Si noti che gli zeta scores sono adimensionali (ovvero, non hanno unità di misura).
Per capire qual è l’effetto di questa normalizzazione, osserviamo le stime di densità dei campioni prima e dopo la normalizzazione:
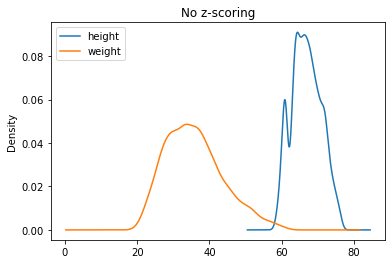
4.3.5. Indicatori di Forma#
Vediamo adesso alcuni indicatori che permettono di farsi un’idea su determinati aspetti della “forma” della distribuzione dei dati.
4.3.5.1. Asimmetria (skewness)#
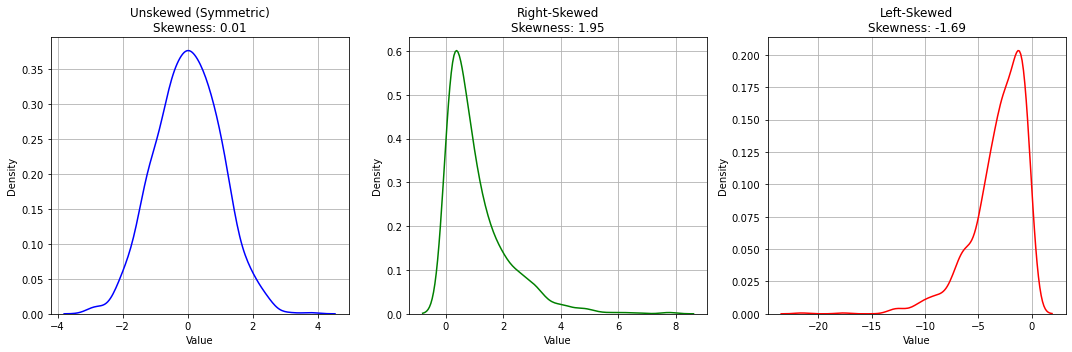
La skewness è indice dello “sbilanciamento” a sinistra (valore negativo) o a destra (valore positivo) di un campione di dati rispetto al valore centrale. La formula della skewness è la seguente:
I valori della skeweness saranno:
Negativi se la distribuzione è sbilanciata a sinistra;
Positivi se la distribuzione è sbilanciata a destra;
Prossimi allo zero in caso di distribuzioni non sbilanciate.
Vediamo degli esempi:
I valori di skewness di pesi e altezze sarnno:
Skweness pesi: 0.57
Skweness altezza: 0.14
4.3.5.2. Curtosi (kurtosis)#
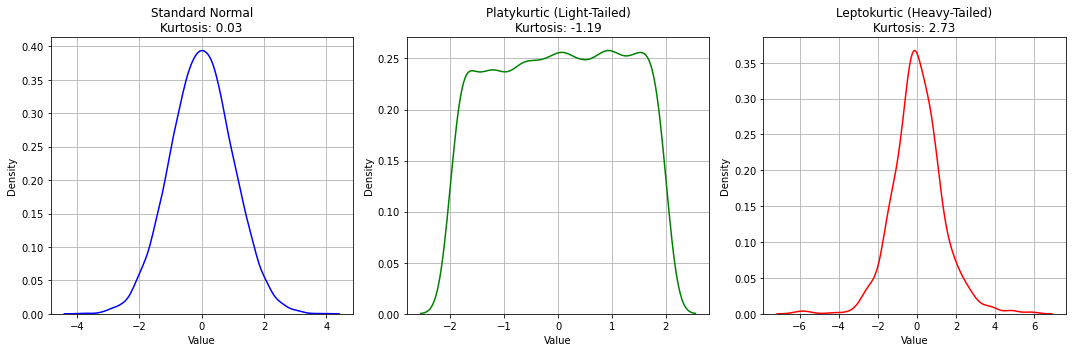
L’indice di curtosi misura lo “spessore” delle code di una misura di densità. Esso è definito come segue:
L’indice va interpretato così:
Se è maggiore di zero, la distribuzione è leptocurtica, ovvero più “appuntita” di una distribuzione Normale;
Se è minore di zero, la distribuzione è platicurtica, ovvero più “piatta” di una distribuzione Normale;
Se è uguale a zero, la distribuzione è normocurtica, ovvero le code sono simili a quelle di una normale.
Vedremo meglio cosa è una funzione normale più in là nel corso. Vediamo degli esempi di valori di Kurtosi:
4.4. Boxplot#
I boxplot costituiscono un metodo di visualizzazione compatto per rappresentare alcune caratteristiche descrittive dei dati sotto analisi. In particolare, dato un campione, un boxplot riesce a rappresentarne efficacemente le seguenti quantità:
Valore mediano;
Primo e terzo quartile;
Minimo e massimo (a seconda della “versione” del boxplot, come discusso di seguito).
Un boxplot si presenta come segue:
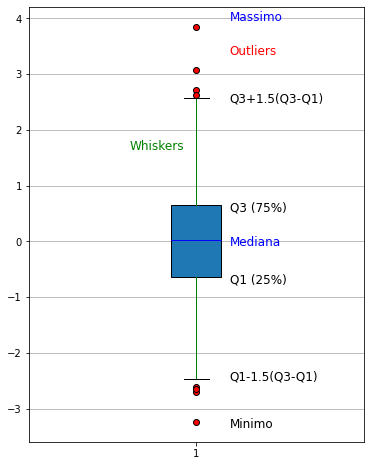
Il boxplot si mostra come una “scatola” con dei “baffi” in cui:
l’estremo inferiore della scatola indica il primo quartile;
l’estremo superiore della scatola indica il terzo quartile;
la linea orizzontale in mezzo alla scatola rappresenta il valore mediano del campione;
il baffo inferiore rappresenta il primo valore nel campione che risulta essere maggiore o uguale al primo quartile meno una volta e mezza la distanza tra i il terzo e il primo quartile;
il baffo superiore rappresenta il primo valore nel campione che risulta essere minore o uguale al terzo quartile più una volta e mezza la distanza tra i il terzo e il primo quartile;
i tondini rappresentano i valori “fuori limite” che ricadono fuori dall’intervallo contrassegnato dai baffi. Vengono in genere considerati come “outliers”.
Per illustrare l’utilità dei boxplot, considereremo il dataset di pesi e altezze visto in precedenza:
| sex | height | weight | |
|---|---|---|---|
| 0 | M | 74 | 53.484771 |
| 1 | M | 70 | 38.056472 |
| 2 | F | 61 | 34.970812 |
| 3 | M | 68 | 35.999365 |
| 4 | F | 66 | 34.559390 |
| ... | ... | ... | ... |
| 4226 | F | 69 | 23.862436 |
| 4227 | M | 69 | 38.262182 |
| 4228 | F | 64 | 34.970812 |
| 4229 | F | 64 | 28.388071 |
| 4230 | F | 61 | 22.628172 |
4231 rows × 3 columns
Mostriamo un il sommario statistico, ovvero la lista di tutti gli indicatori di statistica descrittiva discussi finora:
count 4231.000000
mean 35.818062
std 7.987908
min 20.571066
25% 29.828045
50% 34.970812
75% 41.142132
max 61.301776
Name: weight, dtype: float64
Il boxplot delle altezze si presenta come segue:
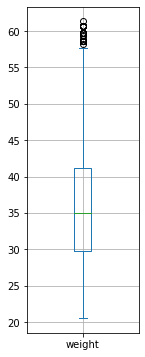
I boxplot possono essere utili a comparare campioni. Ad esempio, i seguenti boxplot comparano le distribuzioni di pesi e altezze:
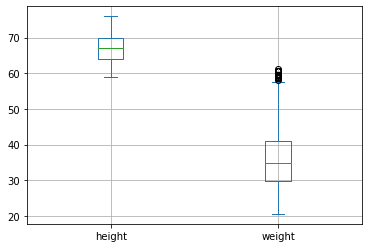
Dal grafico sopra possiamo notare che, mentre weight contiene degli outliers nella parte alta, height non li contiene. Questo non è particolarmente sorprendente, perché è più facile trovare un certo numero di persone sovrappeso che persone molto più alte della norma.
4.5. Referenze#
Capitolo 3 di: Heumann, Christian, and Michael Schomaker Shalabh. Introduction to statistics and data analysis. Springer International Publishing Switzerland, 2016.

