16. Principal Component Analysis#
So far, we have worked with relatively small datasets, with a limited set of interpretable variables. We have seen how models such as linear and logistic regression can help in understanding and interpreting the relationships between variables.
In practice, in many cases, we will work with larger sets of data, where individual variables are not always interpretable. Consider for instance a dataset of medical images with a resolution of \(600 \times 600\) pixels. We may want to be able to apply data analysis to such images, for instance, for automated diagnosis, but, if we think about it, we obtain a set of \(360000\) individual columns. Moreover, such columns are not directly interpretable (each one represent the gray value of a specific pixel in the image).
In most of these cases, the data will be highly redundant, with different variables being dependent or reporting similar data in different forms. Think about it: if there is a large number of variables, it is more likely that some of them capture the same phenomenon from different points of view.
16.1. Feature Selection vs Feature Reduction#
We have seen how, when many variables are available, it makes sense to select a subset of such variables. In regression analysis, in particular, we have seen how, when features are highly correlated, we should discard some of them to reduce collinearity. Indeed, if two variables \(x\) and \(y\) are highly correlated, one of the two is redundant to a given extent, and we can ignore it.
We have seen how variables can be selected in different ways:
By looking at the correlation matrix, we can directly find those pairs of variables which are highly correlated;
When defining a linear or logistic regressor, we can remove those variables with a high p-value. We have seen that these are variables which do not contribute significantly to the prediction of the dependent variable, given all other variables present in the regressor;
Techniques such as Ridge and Lasso regression allow to perform some form of variable (or feature) selection, setting very low or zero coefficients for variables which do not contribute significantly to regression.
In general, however, when we discard a set of variables, we throw away some informative content, unless the variables we are removing can be perfectly reconstructed from the variables we are keeping, e.g., because they are linear combinations of other variables.
Instead of selecting a subset of features to work with, feature reduction techniques aim to find a new set of features which summarize the original set of features losing a small amount of information, while maintaining a limited number of dimensions.
16.2. Feature Reduction Example#
Let us consider the Iris dataset. In particular, we will consider two features: sepal length and petal length:
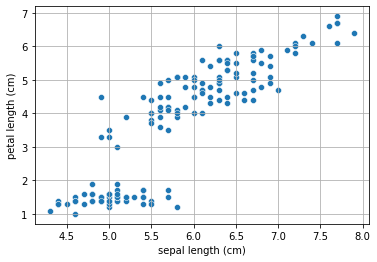
We can see from the plot above that the two features are highly correlated. Let us compute the Pearson coefficient and the related p-value:
PearsonRResult(statistic=0.8717537758865831, pvalue=1.0386674194498827e-47)
Both features represent the length of two physical characteristics of the flowers, hence it is no wonder that they are correlated!. It would be useful to find a transformation of the data \((x_1,x_2)\) into a new set of features \((z_1,z_2)\) such that:
Both \(z_1\) and \(z_2\) are computed from \(x_1\) and \(x_2\), and hence each individual new variable can “summarize” the informative content of both variables;
\(z_1\) and \(z_2\) are sorted by the amount of informative content that they carry about the original variables \((x_1,x_2)\). If this condition is satisfied, then we can select \(z_1\) and discard \(z_2\) to reduce the dimensionality of the original data (from \(2\) to \(1\) variable) while retaining the largest amount of information.
We also note that, ideally, we expect the new variables \(z_1\) and \(z_2\) to be decorrelated. Indeed, if \(z_1\) and \(z_2\) are decorrelated, adding \(z_2\) to the picture only brings additional informative content about the original data, avoiding “repeating” information which is already summarized in \(z_1\).
16.2.1. Rotating Around the Origin#
In our example, we note that a specific rotation of the data around the central point
brings the characteristics highlighted above:
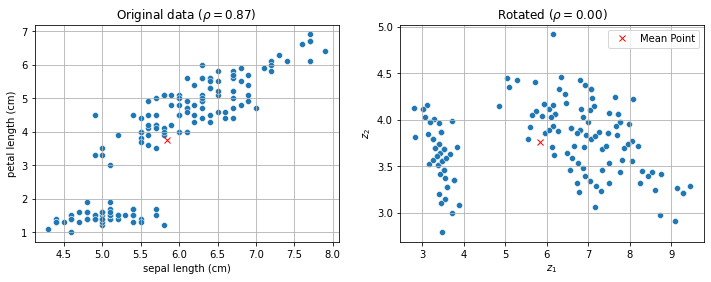
As we can see, this specific rotation (we will see later how to compute the optimal one) has produced a version of the data which is uncorrelated. Note that the rotation around the mean point is a rigid and invertible transformation, hence there is no loss of information.
16.2.2. Amount of Information, Reconstruction Error and Variance#
Without loss of generality, let us now consider the two variables:
These have been obtained by shifting the data to the mean point. Note that this shift has not changed in any way the informative content of the variables.
Since the data has been rotated, we can see the computation of \(z_1\) and \(z_2\) as follows:
Where \(\theta\) is the optimal angle. We will see how to compute the optimal rotation later. For now let us assume that \(\theta=-1.17 rad\) (this is indeed the rotation that has been applied to make the considered set of data uncorrelated).
We can invert the transformation as follows:
If we want to reduce the number of variables, we could either discard \(z_1\) or \(z_2\). If we discard \(z_2\), hence setting it to zero, we can reconstruct the \(x\) and \(y\) values as follows:
If we discard \(z_1\), we obtain:
To have an idea of how much information we lose by discarding one fo the two variables, we can compute the reconstruction error, i.e., the MSE between the predicted and original values. We have:
Another strategy, would be to avoid the transformation altogether and set either \(x=0\) and \(y=0\). We can hence consider other two MSE errors:
In practice, these MSE values will be as follows:
MSE' MSE'' MSEx MSEy
0.139139 3.637486 3.095503 0.681122
As can be seen, reconstructing the data using only \(z_1\) has the least MSE score, suggesting a higher informative content about the original data.
Note that the MSE can also be seen as the sum of the squares of the dashed lines in the following plots:
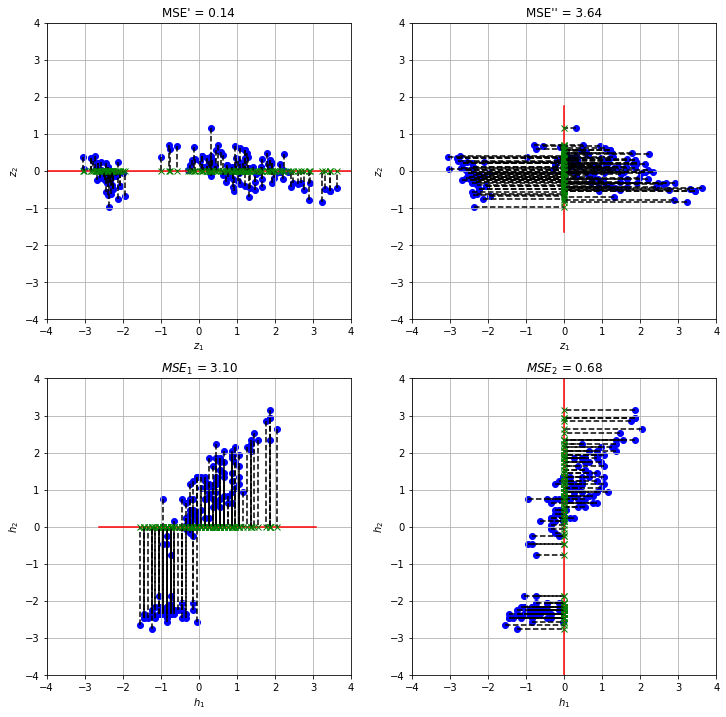
As can be seen, reconstructing the data with the \(z_1\) variable, corresponds to projecting it to the \(z_1\) axis, after the data has been appropriately rotated. This has the lowest error, indicating that \(z_1\) is the most informative single direction.
We can also see that the \(z_1\) variable is the one with the largest variance:
Variance of z1: 3.64
Variance of z2: 0.14
Variance of h1: 0.68
Variance of h2: 3.10
Intuitively, larger variance lends to a larger informative content, and hence to a smaller reconstruction error. Indeed, in variables exhibiting low variance, points tend to be less distinguishable, hence making it harder to reconstruct the original data.
16.2.3. Projection Along a Direction#
Note that we can see the transformation:
As follows:
If we set \(\mathbf{w} = (w_1,w_2)\), \(\mathbf{h}=(h_1,h_2)\), and \(\mathbf{z} = (z_1,z_2)\), we can write:
We also note that \(||\mathbf{w}|| = \sqrt{w_1^2 + w_2^2} = \sqrt{\sin^2\theta + \cos^2 \theta}= 1\).
We recall that the product \(\mathbf{w}^T\mathbf{x}\) corresponds to projecting the point \(\mathbf{x}\) to the unit vector \(\mathbf{w}\) indicating the axis of a new coordinate system.
Indeed:
where \(\theta\) is the angle between the \(\mathbf{w}\) unit vector and the \(\mathbf{x}\) vector. Since \(||\mathbf{w}|| = 1\), we obtain:
This is graphically shown as follows:
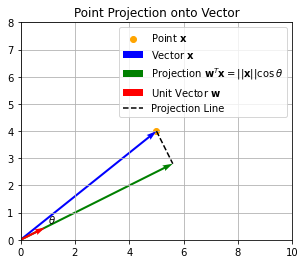
A given choice of a rotation angle \(\theta\) or a vector \(\mathbf{w}\) will hence identify a new direction along which to project all points to obtain the feature \(z_1\), as shown in the following plot:
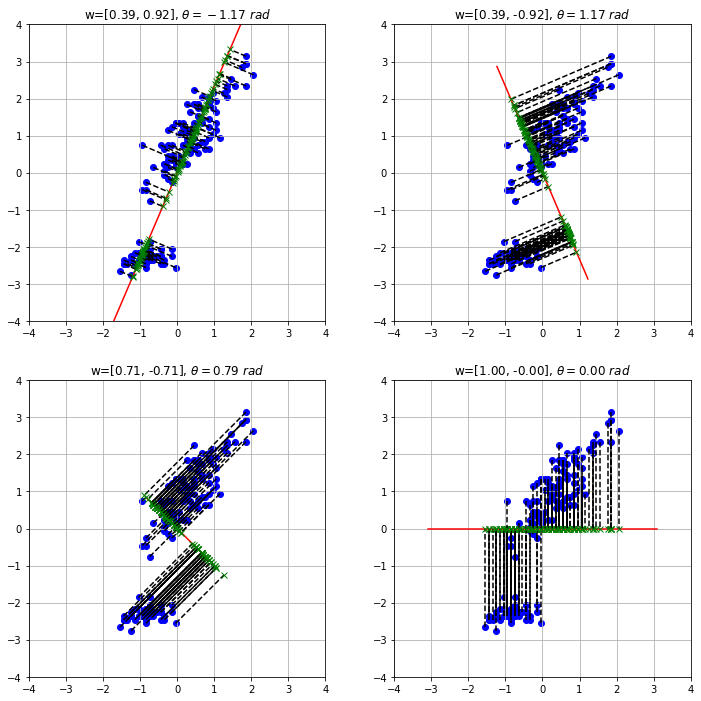
The plots above show how multiplying all points by a vector \(\mathbf{w}\) is equivalent to rotating the data by a given angle, and then projecting the data to the new \(x\) axis. We also note that good projections are the ones that:
Maximize the variance along the \(z_1\) axis;
Minimize the MSE, i.e., the length of the dashed black lines.
16.2.4. An Index to Rule them All#
We can see the variable \(z_1\) found by rotating the data as a single index summarizing the original data. Since it is the single dimension which leads to the smallest reconstruction error, if we have a computational budget of a single variable, it does make sense to represent the data using this value.
Recall that, in the end, \(z_1\) is a linear combination of \(h_1\) and \(h_2\):
We can see \(w_1\) and \(w_2\) as two weights denoting the relative importance of the original variables. If \(h_1\) and \(h_2\) are sepal length and petal length as in our example, \(z_1\) can be seen as a new “largeness” feature and, in this simple example, we may even see it as a way to sort our observations from smaller to larger.
16.3. General Formulation#
We have seen a simple example in the case of two variables. Let us now discuss the general formulation in the case of \(D\)-dimensional variables.
Let \(\{\mathbf{x}_n\}\) be a set of \(N\) observations, where \(n=1,\ldots,N\), and \(\mathbf{x}_n\) is a vector of dimensionality \(D\). We will define Principal Component Analysis as a projection of the data to \(M \lt D\) dimensions such that the variance of the projected data is maximized.
We will first consider the case in which \(M=1\). In this case, we want to find a D-dimensional vector \(\mathbf{u}_1\) such that, projecting the data to this vector, variance is maximized. Without loss of generality, we will choose \(\mathbf{u}_1\) such that \(\mathbf{u}_1^T\mathbf{u}=1\). This corresponds to choosing \(\mathbf{u}_1\) as a unit vector, which makes sense, as we are interested in the direction of the projection. We will find this assumption useful later.
Let \(\overline{\mathbf{x}}\) be the sample mean:
The data covariance matrix \(\mathbf{S}\) will be:
We know that projecting a data point to \(\mathbf{u}_1\) is done simply by the dot product:
The mean of the projected data is hence \(\mathbf{u}_1^T \overline{\mathbf{x}}\), and its variance is:
To find an appropriate \(\mathbf{u}_1\), we need to maximize the variance of the projected data with respect to \(\mathbf{u}_1\). The optimization problem can be formalized as follows:
Note that the constraint \(\mathbf{u}_1^T\mathbf{u}_1=1\) is necessary. Without it, we could arbitrarily increase the variance by choosing vectors \(\mathbf{u}_1\) with large modules, hence \(\mathbf{u}_1^T\mathbf{u}_1 \to +\infty\).
We will not see how this optimization problem is solved in details, but it can be shown that the variance is maximized when:
Note that this is equivalent to:
From the result above, we find out that:
The solution \(\mathbf{u}_1\) is an eigenvector of \(\mathbf{S}\). The related eigenvalue \(\lambda_1\) is the variance along that dimension;
Since we want to maximize the variance, among all eigenvectors, we should choose the one with the largest eigenvalue \(\lambda_1\).
The vector \(\mathbf{u}_1\) will be the first principal component of the data.
We can proceed in an iterative fashion to find the other components. In practice, it can be shown that, to obtain uncorrelated variables, it is convenient to choose the next component \(\mathbf{u}_2\) such that \(\mathbf{u}_2 \perp \mathbf{u}_1\). Doing so, we will form an orthonormal base of the data. We can hence identify the second principal component by choosing the vector \(\mathbf{u}_2\) with maximizes the variance among all vectors which are orthogonal to \(\mathbf{u}_1\).
In practice, it can be shown that the \(M\) principal components can be found by choosing the \(M\) eigenvectors \(\mathbf{u}_1, \ldots, \mathbf{u}_M\) of the covariance matrix \(\mathbf{S}\) corresponding to the largest eigenvectors \(\lambda_1, \ldots, \lambda_M\).
Let us define the matrix \(W\) as follows:
where \(u_{ij}\) is the \(j^{th}\) component of vector \(\mathbf{u}_i\).
Note that, given the way we constructed this matrix, it will be a unit orthonormal matrix. Indeed:
All rows are perpendicular, hence the dot product of any row with any other will be \(\mathbf{u}_i^T \mathbf{u}_j=1\);
The scalar product of any row with itself will be: \(\mathbf{u}_i^T \mathbf{u}_i\)=1;
As a consequence the two conditions above will be valid also for columns;
The determinant of \(\mathbf{W}\) will be 1.
If we choose \(M=D\), we can hence see \(\mathbf{W}\) as a rotation matrix, coherently with our previous interpretation of the PCA. If \(M \lt D\), the matrix \(\mathbf{W}\) identifies a new base for the data.
Let:
be the \([N \times D]\) data matrix.
We can project the data matrix \(X\) to the principal components with the following formula:
\(\mathbf{Z}\) will be an \([N \times M]\) matrix in which the \(i^{th}\) row denotes the \(i^{th}\) element of the dataset projected to the PCA space.
In geometrical terms, the PCA performs a rotation of the D-dimensional data around the center of the data in a way that:
The new axes are sorted by variance;
The projected data is uncorrelated.
16.4. Back to Our Example#
We now have the computational tools to fully understand our example. Let us plot the data again. We will consider the mean-centered data:
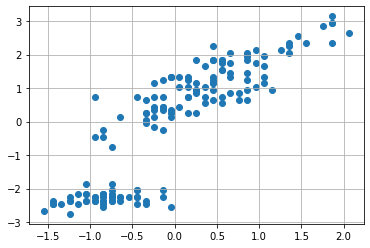
We have seen that the covariance matrix plays a central role in PCA. The covariance matrix will be as follows in our case:
array([[0.68569351, 1.27431544],
[1.27431544, 3.11627785]])
The eigvenvalues and eigenvectors will be as follows:
Eigenvalues: [0.1400726 3.66189877]
Eigenvectors:
[[-0.9192793 0.39360585]
[-0.39360585 -0.9192793 ]]
The rows of the eigenvector matrix identify two principal components. The first one is associated to a variance of about \(0.14\) (the first eigvenvalue), while the second component is associated to a variance of \(3.66\). Let us re-order the principal components so that eigenvalues are descending (we want the first principal component to have the largest value):
Eigenvalues: [3.66189877 0.1400726 ]
Eigenvectors:
[[-0.39360585 -0.9192793 ]
[-0.9192793 0.39360585]]
The two components identify two directions along which we can project our data, as shown in the following plot:
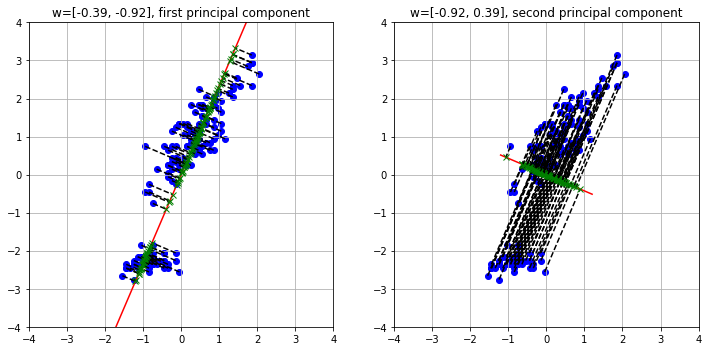
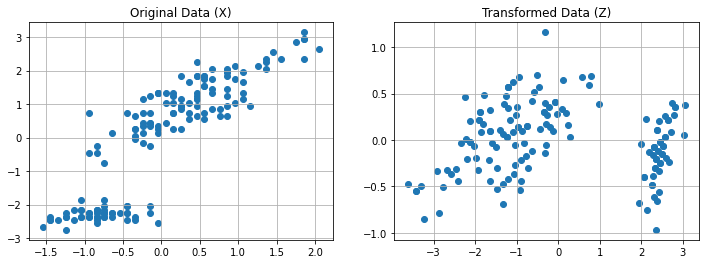
As we can see, the two directions are orthogonal. We can also project the data maintaining the original dimensionality with:
The plot below compares the original and rotated data:
The eigenvectors can also be interpreted as vectors in the original space. Let us show them:
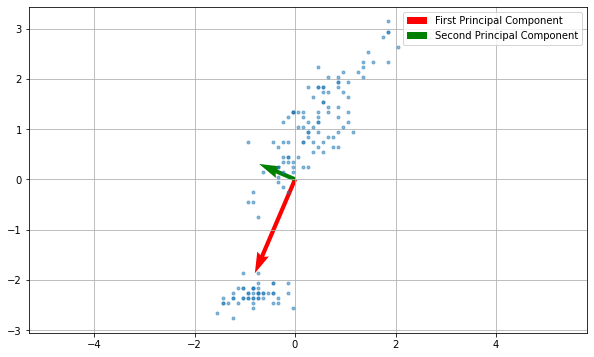
The two principal components denote the main directions of variation within the data. In the plot above, the vector sizes are proportional to the related eigenvalues (hence the variance).
16.5. Choosing an Appropriate Number of Components#
We have seen how PCA allows to reduce the dimensionality of the data. In short, this can be done by computing the first \(M\) eigenvalues and the associated eigenvectors.
In some cases, it is clear what is the value of \(M\) we need to set. For example, in the case of sorting Fisher’s Iris, we set \(M=1\) because we needed a scalar number. In other cases, we would like to reduce the dimensionality of the data, while keeping a reasonable amount of information about the original data.
We have seen that the variance is related to the MSE reprojection error and hence to the informative content. We can measure how much information we are retaining by selecting \(M\) components by measuring the cumulative variance of the first M components.
We will now consider as an example the whole Fisher Iris dataset, which has four features. The four Principal Components will be as follows:
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | |
|---|---|---|---|---|
| components | ||||
| z1 | 0.361387 | 0.656589 | -0.582030 | -0.315487 |
| z2 | -0.084523 | 0.730161 | 0.597911 | 0.319723 |
| z3 | 0.856671 | -0.173373 | 0.076236 | 0.479839 |
| z4 | 0.358289 | -0.075481 | 0.545831 | -0.753657 |
The covariance matrix of the transformed data will be as follows:
| z1 | z2 | z3 | z4 | |
|---|---|---|---|---|
| z1 | 4.23 | 0.00 | -0.00 | 0.00 |
| z2 | 0.00 | 0.24 | -0.00 | -0.00 |
| z3 | -0.00 | -0.00 | 0.08 | 0.00 |
| z4 | 0.00 | -0.00 | 0.00 | 0.02 |
As we could expect, the covariance matrix is diagonal because the new features are decorrelated. We also note that the principal components are sorted by variance. We will define the variance of the data along the \(z_i\) component as:
The total variance is given by the sum of the variances:
More in general, we will define:
Hence \(V=V(D)\).
In our example, the total variance \(V\) will be:
4.57
We can quantify the fraction of variance explained by each component \(n\) as follows:
If we compute such value for all \(n\), we obtain the following vector in our example:
array([0.92461872, 0.05306648, 0.01710261, 0.00521218])
In practice, it is common to visualize the explained variance ratio in a scree plot:
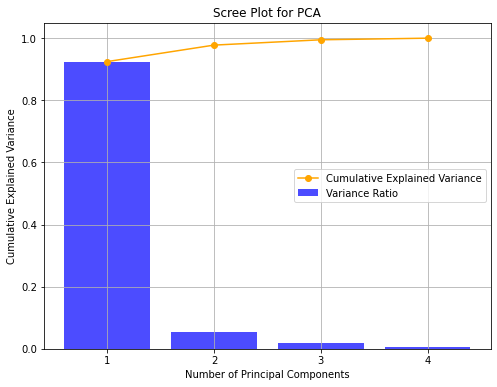
As we can see, the first component retains \(92.46\%\) of the variance, while the second one retains only \(5.3\%\) of the variance. It is common to also look at the cumulative variance ratio, defined as:
In our case:
array([0.92461872, 0.97768521, 0.99478782, 1. ])
The vector above tell us that considering the first two components accounts for about \(97.77\%\) of the variance.
This approach can guide us in choosing the right number of dimensions to keep, selecting a budget of the variance we wish to be able to retain.
16.6. Interpretation of the Principal Components - Load Plots#
When we transform data with PCA, the new variables have a less direct interpretation. Indeed, if a given variable is a linear combination of other variables, it is not straightforward to assign a meaning to each component.
However, we know that the first components are the ones which contain most of the variance. Hence, inspecting the weights that each of these components given to the original features can give some insights into which of the original features are more relevant. In this context, the weights of the principal components are also called loadings. Loadings with large absolute values are more influential in determining the value of the principal components.
In practice, we can assess the relevance of features with a load plot, which represents each original variable as a 2D point of coordinates given by the loadings corresponding to the first two principal components. Let us show the load plot for our example:
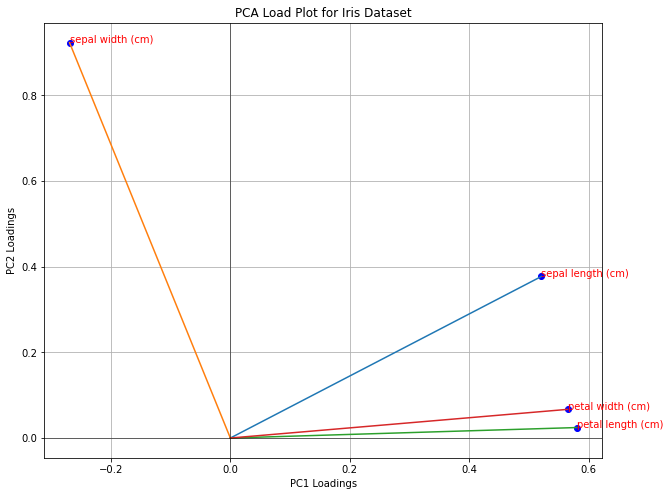
In a load plot:
variables that cluster together are positively correlated, while variables on opposite sides may be negatively correlated;
variables which are further from the origin have higher loadings, so they are more influential in the computation of the PCA.
A loading plot can also be useful to perform feature selection. For instance, from the plot above all variables seem to be influential, but petal width and petal length are correlated. We could think of using as a subset of variables sepal width, sepal length and one of the other two (e.g., petal length).
16.7. Applications of PCA#
PCA has several applications in data analysis. We will summarize the main ones in the following.
16.7.1. Dimensionality Reduction and Visualization#
We have seen that data can be interpreted as a set of D-dimensional points. When \(D=2\), it is often useful to visualize the data through a scatterplot. This allows us to see how the data distributes in the space. When \(D>2\), we can show a series a scatterplot (a pairplot or scattermatrix). However, when \(D\) is very large, it is usually unfeasible to visualize data with all possible scatterplots.
In these cases, it can be useful to transform the data with PCA and then visualize the data points as 2D points in the space identified by the first two principal components.
We will show an example on the multidimensional dataset DIGITS. The dataset contains small images of resolution \(8 \times 8 pixels\) representing handwritten digits from \(0\) to \(9\). We can see the dataset as containing \(64\) variables. Each variable indicates the pixel value at a specific location.
We can visualize the data with PCA by first projecting the data to \(M=2\) principal components, then plotting the transformed data as 2D points.
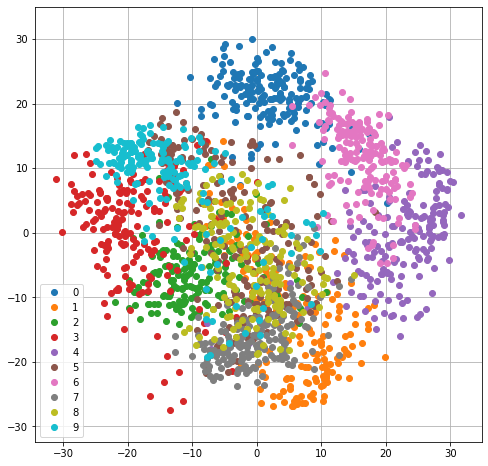
16.7.2. Data Decorrelation - Principal Component Regression#
PCA is also useful when we need to fit a linear regressor and we are in the presence of a dataset with multi-collinearity.
Let us consider the auto_mpg dataset:
| displacement | cylinders | horsepower | weight | acceleration | model_year | origin | mpg | |
|---|---|---|---|---|---|---|---|---|
| 0 | 307.0 | 8 | 130.0 | 3504 | 12.0 | 70 | 1 | 18.0 |
| 1 | 350.0 | 8 | 165.0 | 3693 | 11.5 | 70 | 1 | 15.0 |
| 2 | 318.0 | 8 | 150.0 | 3436 | 11.0 | 70 | 1 | 18.0 |
| 3 | 304.0 | 8 | 150.0 | 3433 | 12.0 | 70 | 1 | 16.0 |
| 4 | 302.0 | 8 | 140.0 | 3449 | 10.5 | 70 | 1 | 17.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 393 | 140.0 | 4 | 86.0 | 2790 | 15.6 | 82 | 1 | 27.0 |
| 394 | 97.0 | 4 | 52.0 | 2130 | 24.6 | 82 | 2 | 44.0 |
| 395 | 135.0 | 4 | 84.0 | 2295 | 11.6 | 82 | 1 | 32.0 |
| 396 | 120.0 | 4 | 79.0 | 2625 | 18.6 | 82 | 1 | 28.0 |
| 397 | 119.0 | 4 | 82.0 | 2720 | 19.4 | 82 | 1 | 31.0 |
398 rows × 8 columns
If we try to fit a linear regressor with all variables, we will find multicollinearity:
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | -17.2184 | 4.644 | -3.707 | 0.000 | -26.350 | -8.087 |
| displacement | 0.0199 | 0.008 | 2.647 | 0.008 | 0.005 | 0.035 |
| cylinders | -0.4934 | 0.323 | -1.526 | 0.128 | -1.129 | 0.142 |
| horsepower | -0.0170 | 0.014 | -1.230 | 0.220 | -0.044 | 0.010 |
| weight | -0.0065 | 0.001 | -9.929 | 0.000 | -0.008 | -0.005 |
| acceleration | 0.0806 | 0.099 | 0.815 | 0.415 | -0.114 | 0.275 |
| model_year | 0.7508 | 0.051 | 14.729 | 0.000 | 0.651 | 0.851 |
| origin | 1.4261 | 0.278 | 5.127 | 0.000 | 0.879 | 1.973 |
Indeed, some variables have a large p-value, probably because they are correlated with the others.
To perform Principal Component Regression, we can first compute PCA on the independent variables, then fit a linear regressor. We will choose \(M=4\) principal components:
| Dep. Variable: | mpg | R-squared: | 0.492 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.487 |
| Method: | Least Squares | F-statistic: | 92.20 |
| Date: | Thu, 14 Dec 2023 | Prob (F-statistic): | 9.24e-55 |
| Time: | 21:38:13 | Log-Likelihood: | -1207.7 |
| No. Observations: | 386 | AIC: | 2425. |
| Df Residuals: | 381 | BIC: | 2445. |
| Df Model: | 4 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 23.3607 | 0.283 | 82.480 | 0.000 | 22.804 | 23.918 |
| z1 | -0.0051 | 0.000 | -15.346 | 0.000 | -0.006 | -0.004 |
| z2 | -0.0320 | 0.007 | -4.373 | 0.000 | -0.046 | -0.018 |
| z3 | -0.0552 | 0.018 | -3.138 | 0.002 | -0.090 | -0.021 |
| z4 | -0.8815 | 0.086 | -10.234 | 0.000 | -1.051 | -0.712 |
| Omnibus: | 3.702 | Durbin-Watson: | 1.125 |
|---|---|---|---|
| Prob(Omnibus): | 0.157 | Jarque-Bera (JB): | 3.435 |
| Skew: | 0.214 | Prob(JB): | 0.179 |
| Kurtosis: | 3.174 | Cond. No. | 860. |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
While the result is not as interpretable as it was before, this technique may be useful in the case of predictive analysis.
16.7.3. Data Compression#
Now let’s see a simple example of data compression using PCA. In particular, we will consider the case of compressing images. An image can be seen as high-dimensional data, where the number of dimensions is equal to the number of pixels. For example, an RGB image of size \(640 \times 480\) pixels has \(3 \cdot 640 \cdot 480=921600\) dimensions.
We expect that there will be redundant information in all these dimensions. One method to compress images is to divide them into fixed-size blocks (e.g., \(8 \times 8\)). Each of these blocks will be an element belonging to a population (the population of \(8 \times 8\) blocks of the image).
Assuming that the information in the blocks is highly correlated, we can try to compress it by applying PCA to the sample of blocks extracted from our image and choosing only a few principal components to represent the content of the blocks.
We will consider the following example image:
Image Size: (427, 640, 3)
Number of dimensions: 819840

We will divide the image into RGB blocks of size \(8 \times 8 \times 3\) (these are \(8 \times 8\) RGB images). These will look as follows:
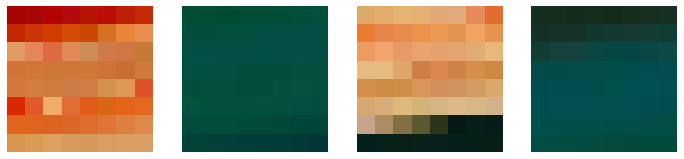
If we compute the PCA of all blocks, we will obtain the following cumulative variance ratio vector:
array([0.72033322, 0.8054948 , 0.88473857, 0.91106289, 0.92773705,
0.94002709, 0.94742984, 0.95262262, 0.95724086, 0.96138203,
0.96493482, 0.96813026, 0.97074765, 0.97304417, 0.97502487,
0.97676849, 0.97827393, 0.97961611, 0.98080084, 0.98195037,
0.98298693, 0.98399279, 0.98491245, 0.98570784, 0.98649079,
0.98719466, 0.98779928, 0.98835152, 0.98888528, 0.98937606,
0.98983658, 0.99027875])
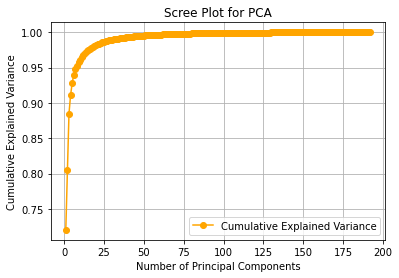
As we can see, truncating at the first component allows us to retain about \(72%\) of the information, truncating at the second allows us to retain about \(80%\), and so on, up to \(32\) components, which allow us to retain about \(99%\) of the information. Now let’s see how to compress and reconstruct the image. We will choose the first \(32\) components, preserving \(99%\) of the information.
If we do so, and then project the tiles to the compressed space each tile will be represented by only \(32\) numbers. This will lead to the following savings in space:
Space saved in the compression: 83.33%
We can reconstruct the original image by applying the inverse PCA transformation to the compressed patches. The result will be as follows:
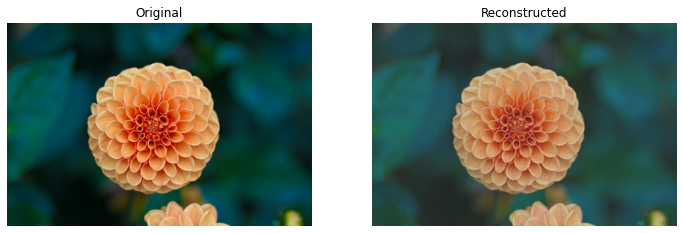
The plot below shows how the reconstruction quality increases when more components are used:

16.8. References#
Parts of Chapter 12 of [1]
[1] Bishop, Christopher M., and Nasser M. Nasrabadi. Pattern recognition and machine learning. Vol. 4. No. 4. New York: springer, 2006.

